update 29-11-2022
 Fig.1 Bron: NOS
Fig.1 Bron: NOS
In juni van dit jaar berichtten alle traditionele media in ons land dat een groep onderzoekers van TU Delft had ontdekt dat de zeespiegel langs de Nederlandse kust steeds sneller stijgt. Daarmee was ‘voor het eerst ‘aangetoond’ dat de zeespiegelstijging langs de Nederlandse kust versnelt, zo schreven de NOS en vele andere media het persbericht na. Maar was dat wel correct?
Voor Marjolein Haasnoot, auteur bij het IPCC en werkzaam bij Deltares, was de uitkomst van het Delftse onderzoek blijkbaar geen verrassing: “… dit soort signalen hebben we wel nodig voor de toekomst. Want we zien nu dat het echt heel veel sneller gaat, en dan moeten we echt ons plan bijstellen. Daar moet je niet te lang mee wachten.” Deltacommissaris Peter Glas, verantwoordelijk voor het deltaprogramma, in het NOS-artikel: “Dit bevestigt de lijn die we al hadden ingezet. Maar dit zit vanaf vandaag ook echt in alle prognoses over wat hoe hoog de dijken en de duinen moeten zijn. Het betekent dat we ons beter en wellicht ook nog sneller moeten aanpassen aan het veranderende klimaat.”
Wetenschappers maar ook bestuurders zouden beter niet zo’n haast moeten hebben, want eerst moet natuurlijk vast komen te staan dat de onderzoeksuitkomsten van het Delftse team correct zijn. De onmiddellijke omarming van de resultaten van het Delftse onderzoek geeft wel duidelijk weer dat ‘zeespiegelstijging’ veel meer is dan een wetenschappelijk onderzoeksobject.
Intussen hebben we al 3 berichten gewijd aan het Delftse onderzoek, zie hier en hier en hier. De conclusie van wat we tot nu toe gevonden hebben is dat de methodiek die de Delftse groep heeft gehanteerd op zijn zachtst gezegd aanvechtbaar is. Maar met een definitief oordeel over de bevindingen van het rapport moesten we wachten tot de onderzoekers de onderliggende data geleverd hadden. En dat is begin oktober uiteindelijk gebeurd. De data zijn de onderliggende data van de kerngrafiek uit de Delftse publicatie, afgebeeld in figuur 2. Die Delftse data en ook de PSMSL meetdata zijn hier te downloaden.
 Fig.2 Bron: Steffelbauer et al (2022)
Fig.2 Bron: Steffelbauer et al (2022)
Figuur 2 is het resultaat van het tweestappenplan dat de onderzoekers ontwikkeld hebben. Stap 1 is het extraheren van het ‘kale’ zeespiegelsignaal uit de gemeten getijdedata. Dat kale signaal zou dan uitsluitend bestaat dan uit data die de sterodynamische (gevolg van zeestromen, temperatuur, zoutgehalte) en barystatische (watermassa) veranderingen van de zeespiegel weergeven. Stap 2 is het opsporen van een mogelijke versnelling in het in stap 1 geëxtraheerde signaal van het zeeniveau.
Stap 1: extractie van het Delftse zeeniveau-signaal
De onderzoekers gaan uit van de idee dat de gemeten zeespiegelhoogte op een bepaalde plaats de resultante is van het hierboven beschreven ‘kale’ zeespiegelsignaal, plus daar bovenop seizoenschommelingen (jaarlijkse seizoenen en de nodale cyclus), externe invloeden (luchtdruk, zonale windstress en meridionale windstress) en ‘irregular component’ . De idee is nu dat als je die effecten van het gemeten signaal ‘afpelt’ dat je dan het ‘echte’ zeespiegelsignaal krijgt.
Over de nodale cyclus is al voldoende geschreven in deel 3 van de analyse. Spil in de Delftse methodiek is de invloed van de wind op de getijdemetingen. De Delftse onderzoekers maken daarvoor gebruik van de winddata van reanalyses van NOAA, waarbij de wind per rastercel opgedeeld is in een zonale en een meridionale component.
 Fig.3 Bron: Linkedin
Fig.3 Bron: Linkedin
Hessel Voortman, expert op het gebied van kustverdediging, reageerde via Twitter op het Delftse rapport (figuur 3). Volgens Voortman is het gebruik van zonale en meridionale windstress-data zoals gebruikt door de auteurs voor het corrigeren van de getijdemeetreeksen onjuist, omdat de vorm van het Noordzeebekken het windeffect sterk richtinggevoelig maakt. Het proefschrift van Voortman levert interessant leesvoer op dit vlak. Ongetwijfeld gaan we op korte termijn nog meer horen en lezen over deze cruciale windstressfactor.
De Delftse onderzoekers haalden tenslotte de ruis uit het overgebleven signaal. Uit de beschrijving in de paper werd me niet duidelijk hoe dat is gebeurd. Statistisch bezien lijkt het niet geoorloofd om vervolgens die ruis te negeren bij het bepalen van trends. Dat is een groot probleem, omdat een trendbreuk alleen al daardoor significant kan worden. Daarover later meer.
 Fig.4 Bron: Steffelbauer et al (2022)
Fig.4 Bron: Steffelbauer et al (2022)
Figuur 4 laat de grafieken van de diverse hiervoor beschreven componenten zien die in mindering gebracht zijn op de gemeten getijdedata. Het effect daarvan op het gemeten PSMSL signaal ziet er voor Vlissingen zo uit:

Fig.5 Data: PSMSL en Steffelbauer et al
De blauwe lijn toont de maandelijkse gemeten zeespiegeldata van station Vlissingen, de bruine lijn toont de door het Delftse team berekende ‘kaalgeplukte’ sea level signal van Vlissingen. Te zien is dat de oorspronkelijke PSMSL zeespiegeldata door de onderzoekers zo sterk ‘gecorrigeerd’ zijn, dat de ruis (variantie) nagenoeg verdwenen is. Dat veroorzaakt volgens deskundigen een grote toename van de kans op een significant trendverschil in de Delftdata in vergelijking met de gemeten PSMSL-data.
Stap 2: opsporen van breukpunten
In de abstract van de publicatie schrijven de onderzoekers: “We applied the approach to eight 100-year records in the southern North Sea and detected, for the first time, a common breakpoint in the early 1990s. The mean SLR rate at the eight stations increases from 1.7 ± 0.3 mm yr−1 before the breakpoint to 2.7 ± 0.4 mm yr−1 after the breakpoint (95% confidence interval), which is unprecedented in the regional instrumental record.”
 Fig.6 Data: Steffelbauer et al
Fig.6 Data: Steffelbauer et al
Het onderzoeksteam van TU Delft claimt een trendbreuk in alle onderzochte stations begin jaren ’90 van de vorige eeuw. Figuur 6 toont de detrended zeespiegelsignalen voor de 6 hoofdstations zoals Delft die berekend heeft. Het verwijderen van de langjarige trend over de hele reeks maakt trendbreuken makkelijker visueel op te sporen en is toelaatbaar omdat het hier gaat om trendverschillen. De bruine lijn is een loess smoothing. Die loess smooothing laat zien dat de ‘sea level signals’ van Delft na 1993 wél een versnelling in Delfzijl en Harlingen tonen en een lichte stijging in Vlissingen, maar géén versnelling in Den Helder, IJmuiden en Hoek van Holland.
Dat de Waddenzeestations Harlingen en Delfzijl in de Delftse data een wat andere positie innemen dan de andere stations zou wel eens te maken kunnen hebben met hun ligging en de geografische oriëntatie op het noorden. De door Voortman aangehaalde richtinggevoeligheid voor het windeffect zou dan een rol kunnen spelen.
Die ‘early 1990’s ’ uit het citaat van de abstract zijn om precies te zijn de 11 maanden vóór augustus 1993 tot en met de 11 maanden erna, van september 1992 t/m juli 1994. Omdat ik alleen geïnteresseerd was in data van de Nederlandse kuststations heb ik mijn aandacht beperkt tot de 6 hoofdstations, te weten Delfzijl, Harlingen, Den Helder, IJmuiden, Hoek van Holland en Vlissingen. Cuxhaven (Duitsland) en Maassluis (geen kuststation), die wel in het Delftse onderzoek meegenomen worden, bekeek ik dus niet.
 Fig.7
Fig.7
Aan de hand van de door Steffelbauer aangeleverde sea level signal data hebben we voor de periode januari 1919 t/m december 2018 voor elke maand de trend bepaald van de interval vanaf 1919 tot de breukmaand (k1) en van de interval vanaf de breukmaand t/m 2018 (k2). Zie figuur 7.
 Fig.8
Fig.8
Steffelbauer neemt voor elk van de 6 stations breuken waar, in de periode van 11 maanden vóór augustus 1993 tot 11 maanden na augustus 1993. Figuur 8 toont per station de reeksen van de Delftse onderzoekers plus de trendlijnen van de interval 1919 tot augustus 1993 (k1) en van augustus 1993 t/m 2018 (k2).
Er valt direct een tweetal zaken op. In de eerste plaats is de trend van k2 van IJmuiden niet hoger maar lager dan van k1. In de tweede plaats wijken de k2 trends van Hoek van Holland en Den Helder nauwelijks af van de k1 trends van diezelfde stations. Dat laatst zou kunnen betekenen dat er op die stations geen sprake is van een significante breuk, maar dat moet nader onderzocht worden. Dat k2 van IJmuiden een trend vertoont die lager is dan k1 komt niet overeen met de claim van het Delftse team dat er sprake is van een ‘common breakpoint’.
 Fig.9
Fig.9
Figuur 9 toont de grafiek van IJmuiden uit de paper van Steffelbauer (onder) en onze reconstructie op basis van de Steffelbauer-data (boven) met als breukmaand augustus 1993. Duidelijk is te zien dat in de reconstructie in IJmuiden de trendlijn van k2 (bruine lijn) lager ligt dan die van k1 (doorgetrokken blauwe lijn). Op station IJmuiden neemt dus na het breukjaar de zeespiegeltrend af in plaats van toe.
De grafiek van figuur 9 boven is gebaseerd op een breuk in augustus 1993. Nu kan het natuurlijk ook zijn dat de cijfers van IJmuiden (en andere stations) wat anders komen te liggen als men niet augustus 1993 neemt als breekpunt maar een van de 2x 11 maanden daar rondom heen. Ik heb dat uitgezocht voor elke maand in de periode sep 1992 t/m juli 1994 en er een grafiek van gemaakt:
 Fig.10
Fig.10
De grafiek toont het verschil tussen k2-k1 voor elk station. Maand 12 is augustus 1993. De uitkomst in IJmuiden is voor elk van de 23 maanden negatief. Bovendien is te zien dat voor station Hoek van Holland het trendverschil in de laatste 3 maanden ook negatief is. Ook is goed te zien dat de trendverschillen van Den Helder en Hoek van Holland voor en na de ‘breuk’ erg dicht bij 0 liggen, zoals al eerder geconstateerd is. Wellicht dat we op een later moment kunnen kijken hoe het zit met de significantie van die trendbreuken.
 Fig.11
Fig.11
De tabel van figuur 11 laat de trendwaarden zien voor en na de breuk in elk van de 23 maanden rond augustus 1993, berekend op basis van de data van Steffelbauer. De grafiek van figuur 10 is gebaseerd op deze tabel. Opvallend is dat voor alle 6 hoofdstations k1 en k2 afwijken van de cijfers die in de publicatie gegeven worden (figuur 12):
 Fig.12
Fig.12
“…detected, for the first time, a common breakpoint in the early 1990s.” Hierboven is al duidelijk gemaakt dat dat ‘common’ in de abstract niet terecht is, het Delftse sea level signal van IJmuiden heeft immers na het breekpunt een lagere trend dan ervoor. Maar ook rond 2001/2002 zie ik in de grafieken van figuur 6 mogelijke breekpunten.
Intussen is er in de wereld van Waterbouw een soort van stammenoorlog uitgebroken tussen de ‘rekkelijken’ en de ‘preciezen’. De rekkelijken zijn dan mensen als Marjolijn Haasnoot van Deltares en Deltacommissaris Peter Glas die met name actief zijn op het gebied van watermanagement. Deze mensen hebben blijkbaar maar een half woord nodig om in de alarmistische stand te schieten, zoals hun uitspraken in het NOS-artikel van 27 juni 2022 laten zien.
De preciezen zijn de waterbouw-ingenieurs die goed kunnen rekenen en in ons land van oudsher gaan over kustbeveiliging. Zij gaan uit van meetgegevens en zijn vaak minder gevoelig voor maatschappelijke druk en hypes. Een bekende naam is professor Bas Jonkman van TU Delft die vorige maand de knuppel in het hoenderhok gooide met een post op LinkedIn, Enfin, dat mondde uit in een artikel over de kwestie in het NRC.

Fig.13 Bron: NRC
De ingenieurs houden het beschaafd, maar de boodschap is duidelijk: onnodige bangmakerij. Juist omdat het onderwerp ’zeespiegelstijging’ zeer gevoelig ligt in deze tijd van klimaathysterie is het extra nodig dat de cijfers over die stijging kloppen, lijkt me. De conclusies van Steffelbauer et al voldoen daar volgens mij niet aan.
Er zijn voldoende aanwijzingen dat de uitkomsten van Steffenbauer’s publicatie niet serieus te nemen zijn. Het verhaal rammelt. Van een ‘gemeenschappelijk breekpunt’ is geen sprake, en het verwijderen van ruis maakt de overblijvende reeks uiterst gevoelig voor trendbreuken. Het team heeft daardoor mogelijk zijn eigen trendbreuken geschapen. Het ‘sea level signal’ in de Delftse publicatie is de uitkomst van een interessante wetenschappelijke exercitie, maar heeft weinig met het echte zeeniveau te maken.
De auteurs schrijven: “The mean SLR rate at the eight stations increases from 1.7 ± 0.3 mm yr−1 before the breakpoint to 2.7 ± 0.4 mm yr−1 after the breakpoint (95% confidence interval), which is unprecedented in the regional instrumental record.”
Hier is echter geen sprake van een mean SLR rate maar van een kunstmatige cijferreeks. Die vermeende stijging van de trend na 1993 1,7 mm/jaar naar 2,7 mm/jaar is het product van die cijferreeks. En dat “unprecedented in the regional instrumental record” is onzin: de cijferreeks van Steffelbauer is géén regional instrumental record. Dat zijn alleen de gemeten data van Rijkswaterstaat/PSMSL. Dit zijn ze, op hun volle lengte van 1890 t/m 2021 met lineaire trends plus versnellingen:
 Fig. 14 Bron: sealevel.info
Fig. 14 Bron: sealevel.info
Te zien is dat er in die 132 jaren nauwelijks sprake is van een versnelling in de tijdreeksen van de 6 stations. Dat is des te opmerkelijker, omdat er voortdurend grootschalige menselijke activiteiten aan onze kustlijn hebben plaatsgevonden. Ik denk aan de uitdieping van de Westerschelde, de aanleg van de Deltawerken, de uitbreiding en verdieping van de Rotterdamse haven, de aanleg van de Afsluitdijk en de delfstofwinning nabij Hoek van Holland en vooral in de noordelijke provincies.
De meeste van die activiteiten hebben op een of andere manier invloed op de zeespiegel. Hoevéél is onderwerp van onderzoek. Voor de gaswinning in Groningen is in elk geval bekend dat sinds 1963 de bodem nabij Delfzijl met maar liefst 24 cm gedaald is (zie figuur 16, bron Deltares). Intussen heb ik begrepen dat de PSMSL data voor die bodemdaling door gaswinning worden gecorrigeerd.
 Fig. 15 Bron: Zeespiegelmonitor 2018
Fig. 15 Bron: Zeespiegelmonitor 2018
 Figuur 1. Puntenwolk, oppervlaktetemperatuur per rastercel versus beschikbaar zonne-energie. Aantal rastercellen = 64.800. De cyaan/zwarte lijn toont de LOESS smoothing van de gegevens. De helling van de cyaan/zwarte lijn toont de verandering in temperatuur voor elke verandering van 1 W/m2 in beschikbare zonne-energie. De gegevens in dit bericht zijn gemiddelden van de volledige 21 jaar CERES-gegevens.
Figuur 1. Puntenwolk, oppervlaktetemperatuur per rastercel versus beschikbaar zonne-energie. Aantal rastercellen = 64.800. De cyaan/zwarte lijn toont de LOESS smoothing van de gegevens. De helling van de cyaan/zwarte lijn toont de verandering in temperatuur voor elke verandering van 1 W/m2 in beschikbare zonne-energie. De gegevens in dit bericht zijn gemiddelden van de volledige 21 jaar CERES-gegevens. Figuur 2. Beschikbare zonne-energie (TOA-zonnestraling minus albedo-reflecties), het bovenste kaartje is een projectie met de Stille Oceaan in het midden, het onderste kaartje met de Greenwich meridiaan in het midden. Gebieden in rood omlijnd met cyaan/zwart veranderen niet van temperatuur bij verhoogde gemiddelde zonne-input. Poolgebieden in blauw omlijnd met wit/zwart tonen waar de temperatuur zeer gevoelig is voor verhoogde zonne-input. De gestippelde horizontale lijnen zijn de keerkringen en poolcirkels.
Figuur 2. Beschikbare zonne-energie (TOA-zonnestraling minus albedo-reflecties), het bovenste kaartje is een projectie met de Stille Oceaan in het midden, het onderste kaartje met de Greenwich meridiaan in het midden. Gebieden in rood omlijnd met cyaan/zwart veranderen niet van temperatuur bij verhoogde gemiddelde zonne-input. Poolgebieden in blauw omlijnd met wit/zwart tonen waar de temperatuur zeer gevoelig is voor verhoogde zonne-input. De gestippelde horizontale lijnen zijn de keerkringen en poolcirkels. Figuur 3. Helling van de trendlijn in figuur 1. Dit toont de temperatuurverandering bij een verandering van 1 W/m2 in de beschikbare instraling.
Figuur 3. Helling van de trendlijn in figuur 1. Dit toont de temperatuurverandering bij een verandering van 1 W/m2 in de beschikbare instraling. Figuur 4. Zoals in figuur 3, maar met 21 afzonderlijke jaren in plaats van een gemiddelde over 21 jaar.
Figuur 4. Zoals in figuur 3, maar met 21 afzonderlijke jaren in plaats van een gemiddelde over 21 jaar.


 Figuur 3. LOESS smooths van de puntenwolken van vier geselecteerde subsets van de CERES-gegevens. De onderliggende puntenwolkgegevens worden niet getoond.
Figuur 3. LOESS smooths van de puntenwolken van vier geselecteerde subsets van de CERES-gegevens. De onderliggende puntenwolkgegevens worden niet getoond.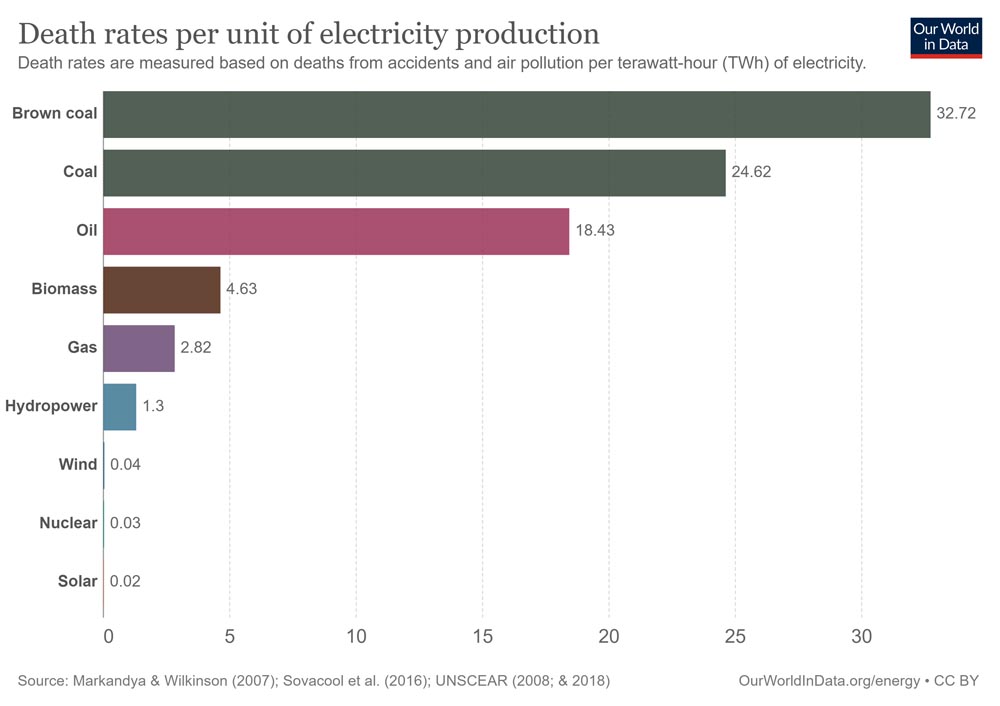 Fig.1 Bron:
Fig.1 Bron: 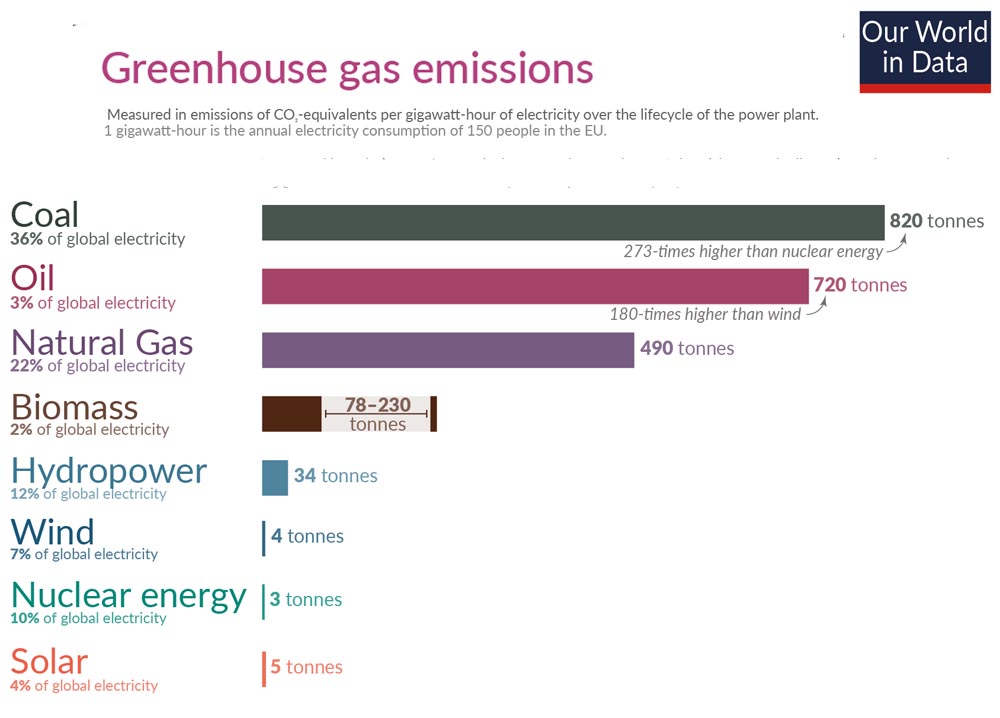 Fig.2 Bron: Ourworldindata
Fig.2 Bron: Ourworldindata Fig.3 Bron: Ourworldindata
Fig.3 Bron: Ourworldindata Fig.1 Bron:
Fig.1 Bron: 
 Fig.3 Bron: Linkedin
Fig.3 Bron: Linkedin Fig.4 Bron: Steffelbauer et al (2022)
Fig.4 Bron: Steffelbauer et al (2022)
 Fig.6 Data: Steffelbauer et al
Fig.6 Data: Steffelbauer et al Fig.7
Fig.7 Fig.8
Fig.8 Fig.9
Fig.9 Fig.10
Fig.10 Fig.11
Fig.11 Fig.12
Fig.12
 Fig. 14 Bron:
Fig. 14 Bron:  Fig. 15 Bron:
Fig. 15 Bron: 
 Fig.1 Veranderingen in de oppervlaktetemperatuur, CERES-gegevens. Dit is een omrekening van de CERES-gegevens van de naar boven gerichte langgolvige straling aan het oppervlak naar graden Celsius met behulp van de Stefan-Boltzmann-vergelijking. Het komt goed overeen met bijvoorbeeld de LTL data van satellietmetingen in de tropen, met een resterende standaardfout van ongeveer een tiende graad C.
Fig.1 Veranderingen in de oppervlaktetemperatuur, CERES-gegevens. Dit is een omrekening van de CERES-gegevens van de naar boven gerichte langgolvige straling aan het oppervlak naar graden Celsius met behulp van de Stefan-Boltzmann-vergelijking. Het komt goed overeen met bijvoorbeeld de LTL data van satellietmetingen in de tropen, met een resterende standaardfout van ongeveer een tiende graad C. Fig. 2 Broeikasversterking. De versterking wordt berekend als de opwaartse langgolvige oppervlaktestraling gedeeld door de inkomende zonnestraling (na albedo-reflecties). Een versterkingsfactor van 2 betekent dat het oppervlak twee keer méér energie uitstraalt (langgolvige straling in W/m2)voor elke W/m2 zonne-energie die daadwerkelijk binnenkomt. Hieruit blijkt dat het broeikaseffect de inkomende zonnestraling met ongeveer twee derde heeft verhoogd, gemeten aan het oppervlak.
Fig. 2 Broeikasversterking. De versterking wordt berekend als de opwaartse langgolvige oppervlaktestraling gedeeld door de inkomende zonnestraling (na albedo-reflecties). Een versterkingsfactor van 2 betekent dat het oppervlak twee keer méér energie uitstraalt (langgolvige straling in W/m2)voor elke W/m2 zonne-energie die daadwerkelijk binnenkomt. Hieruit blijkt dat het broeikaseffect de inkomende zonnestraling met ongeveer twee derde heeft verhoogd, gemeten aan het oppervlak. Fig. 3 Opwaartse warmtestraling aan het oppervlak (geel, linkerpaneel), en inkomende zonnestraling na albedo-reflecties (rood, rechterpaneel). De blauw/zwarte lijnen zijn LOWESS-smoothing van de gegevens.
Fig. 3 Opwaartse warmtestraling aan het oppervlak (geel, linkerpaneel), en inkomende zonnestraling na albedo-reflecties (rood, rechterpaneel). De blauw/zwarte lijnen zijn LOWESS-smoothing van de gegevens. Fig. 4 Temperatuur (geel, linkerschaal) en opwaartse langgolvige straling aan het oppervlak (rood, rechterschaal)
Fig. 4 Temperatuur (geel, linkerschaal) en opwaartse langgolvige straling aan het oppervlak (rood, rechterschaal)

 Figuur 1: Correlatie per rastercel van geabsorbeerde straling (kortgolvig + langgolvig) en oppervlaktetemperatuur. Rastercellen zijn 1° breedtegraad x 1° lengtegraad.
Figuur 1: Correlatie per rastercel van geabsorbeerde straling (kortgolvig + langgolvig) en oppervlaktetemperatuur. Rastercellen zijn 1° breedtegraad x 1° lengtegraad.
 Figuur 3. Scatterplot, waarbij elke stip een maand is. Voor elke maand toont de x-as de geabsorbeerde straling van die maand, en de y-as de temperatuur van diezelfde maand.
Figuur 3. Scatterplot, waarbij elke stip een maand is. Voor elke maand toont de x-as de geabsorbeerde straling van die maand, en de y-as de temperatuur van diezelfde maand. Figuur 4. Geabsorbeerde totale straling aan het oppervlak (blauw, rechter schaal) versus temperatuur (rood, linker schaal). De totale straling is de som van de neerwaartse langgolvige straling van de atmosfeer, plus de kortgolvige zonnestraling. Ook de theoretische toename van CO2- forcering over de periode (geel/zwarte lijn) en de trend van de totale geabsorbeerde straling (gestippelde cyaan/zwarte lijn) zijn ingetekend. De gestippelde horizontale zwarte lijn laat zien wat er zou gebeuren als de geabsorbeerde straling aan het oppervlak niet zou toenemen.
Figuur 4. Geabsorbeerde totale straling aan het oppervlak (blauw, rechter schaal) versus temperatuur (rood, linker schaal). De totale straling is de som van de neerwaartse langgolvige straling van de atmosfeer, plus de kortgolvige zonnestraling. Ook de theoretische toename van CO2- forcering over de periode (geel/zwarte lijn) en de trend van de totale geabsorbeerde straling (gestippelde cyaan/zwarte lijn) zijn ingetekend. De gestippelde horizontale zwarte lijn laat zien wat er zou gebeuren als de geabsorbeerde straling aan het oppervlak niet zou toenemen.

 Figuur 4. Maandelijkse variaties in het oceaangebied waar de temperatuur en de geabsorbeerde straling negatief gecorreleerd zijn.
Figuur 4. Maandelijkse variaties in het oceaangebied waar de temperatuur en de geabsorbeerde straling negatief gecorreleerd zijn.