Vraag 10 mensen wat het belangrijkste broeikasgas is en tenminste 9 zullen CO2 antwoorden. Fout dus. Het belangrijkste broeikasgas is H2O, in de vorm van waterdamp en wolken. Kooldioxide vormt, zoals gezegd, 0,038% van de atmosfeer, terwijl water in zijn verschillende vormen varieert van 0% tot 4% van de atmosfeer. Kort gezegd: het grootste deel van het broeikaseffect wordt veroorzaakt door H2O als gevolg van de overvloedige aanwezigheid ervan in de atmosfeer. Water is goed voor ongeveer 90% van het broeikaseffect : ongeveer 70% is te wijten aan waterdamp en ongeveer 20% aan wolken (meestal waterdruppels).
Sommige schattingen over de werkzaamheid van water als broeikasgas reiken zelfs zo hoog als 95% van het totale troposferisch broeikaseffect ( e.g., Freidenreich and Ramaswamy, “Solar Radiation Absorption by Carbon Dioxide, Overlap with Water, and a Parameterization for General Circulation Models,” Journal of Geophysical Research 98 (1993):7255-7264). Het resterende deel komt van kooldioxide (CO2), lachgas, methaan, ozon en diverse andere “kleine broeikasgassen.” Als een voorbeeld van het relatieve belang van water moet worden opgemerkt dat veranderingen in de relatieve vochtigheid op de orde van grootte van 1,3 – 4% gelijk staat aan het effect van de verdubbeling van CO2.
Gezien de huidige samenstelling van de atmosfeer is de bijdrage aan de totale verwarming in de troposfeer (het onderste deel van de atmosfeer, 0-10 km, waarin zich de belangrijkste weersprocessen afspelen) ongeveer 5% door kooldioxide en ongeveer 95% door waterdamp. In de stratosfeer (10-50 km) echter is de bijdrage ongeveer 80% door kooldioxide en ongeveer 20% door waterdamp, maar in dit deel van de atmosfeer levert het slechts een relatief kleine bijdrage aan het totale broeikaseffect.
Het netto broeikaseffect voor de totale atmosfeer wordt derhalve voor ongeveer 90% bepaald door H2O (in de vorm van waterdamp en wolkendruppels) en 10% CO2 en andere broeikasgassporen.Overigens variëren de cijfers sterk, afhankelijk van onder andere de breedteligging. De verhouding 90% : 10% betreft het wereldwijde jaarlijkse netto broeikaseffect van de totale atmosfeer.
Bovenstaande figuur geeft een beeld van de diverse golflengtes en bandbreedtes waarop broeikasgassen straling absorberen. Daar waar een donker vlak tot de bovenliggende lijn doorloopt absorbeert het gas de betreffende golflengtes volledig.
In de grafiek hierboven is de totale absorptie in de atmosfeer weergegeven, dus zowel in het infrarood gebied als in het gebied van de kortgolvige zonnestralen. Van de 33° C temperatuurverhoging van de troposfeer als gevolg van het broeikaseffect komt ruwweg 21° C voor rekening van waterdamp. Waterdamp absorbeert sterk in de banden 2,4 – 3,1 µm, 4,5 – 6,5 µm en boven de 16 µm. Voor CO2 is de belangrijkste absorptieband gelegen bij 14 – 16 µm, maar er zijn ook absorptiebanden bij 2,6 µm en 4,2 µm.
Daar waar in het infrarode spectrum waterdamp en CO2 niet werkzaam zijn als absorptiemedium, zoals in de nabijheid van 10 µm golflengte, ontsnapt langgolvige straling ongehinderd de ruimte in. Het gebied van 8,5 – 13 µm is het zogenaamde atmosferische venster.
Waar infrarood straling geabsorbeerd wordt door broeikasgassen, nemen de moleculen de energie op , raken in trilling, en stralen ze de energie vrijwel onmiddellijk weer in alle richtingen uit. Uiteindelijk wordt de energie op deze manier naar de rand van de dampkring getransporteerd, waar het de ruimte in verdwijnt.
In onderstaande figuur is te zien dat van de totale uitstraling van warmte een kleine 20% de ruimte in verdwijnt via het atmosferisch venster, terwijl de rest uitgestraald wordt door waterdamp, CO2 en wolken.
Omdat de band rond 15 µm vrijwel verzadigd is, zal een stijgend CO2 gehalte slechts een stijging van absorptie veroorzaken in de smalle banden van 2,6 en 4,2 µm. Wat dit voor consequenties heeft wordt op de volgende pagina nader beschreven.
CO2 is tamelijk gelijkmatig verspreid over de atmosfeer, dus is het aannemelijk dat CO2 een relatief groter effect moet hebben op de luchttemperatuur in regio’s waar de hoeveelheid waterdamp gering is, zoals woestijnen en Arctische gebieden.
In gebieden met relatief veel waterdamp, zoals de tropen en een groot deel van de gematigde zone, is het effect van CO2 gering in vergelijking met dat van waterdamp.
Onderstaande figuur is uit de dissertatie van Rob van Dorland, en toont het effect van diverse broeikasgassen op de kortgolvige en langgolvige straling, op diverse hoogtes. De figuur is ontleend aan een publicatie van S.Manabe en R.F.Strickler.
Op de horizontale as staat de invloed op de stralingsbalans in K/dag. Geen invloed is 0. Negatieve tendensen hebben een afkoelend effect, positieve een opwarmend effect. Interessant is de top in de grafiek van L CO2 op ongeveer 2,5 km hoogte. Dit voorspelde ´warmte-eiland´ is nog niet waargenomen.
De theorie
De term “broeikaseffect” is eigenlijk slecht gekozen. Een echte kas belemmert weliswaar – net als broeikasgassen dat doen- de uitstraling van een deel van de langgolvige warmtestraling, maar verhindert ook convectie van warme lucht, terwijl in de atmosfeer convectie een zeer belangrijk proces is. Het broeikaseffect is nodig om de aarde leefbaar te houden. Om te begrijpen wat het betekent als het broeikaseffect en atmosfeer ontbreekt hoef je maar naar de maan te kijken. De gemiddelde temperatuur gedurende een “maandag” is 107 °C , de temperatuur in de “maannacht” daalt tot -153 °C. De temperatuur op aarde met atmosfeer en wolken, maar zonder broeikaseffect, wordt geschat op -18 °C (255 K) Het broeikaseffect verhoogt de temperatuur van de aarde met ongeveer 32 °C.
De zon, die veel warmer is dan de aarde, zendt kortgolvige straling uit, terwijl de aarde langgolvige straling uitzendt. Hoe koeler de aarde of de atmosfeer, des te lager de energie-intensiteit, en des te groter de golflengte van de uitgezonden straling.
Broeikasgassen zijn in het algemeen doorlaatbaar voor inkomende zonnestraling (ze laten de meeste zonnestraling door) en (deels) ondoorlaatbaar voor aardse warmtestraling (ze absorberen en emitteren de warmtestraling). Maar zuurstof en ozon absorberen inkomende ultraviolette (UV) straling (<0.3μm), en water, ozon, zuurstof en, in mindere mate kooldioxide, absorberen ook een kleine hoeveelheid inkomende kortgolvige straling < 3 micron (micrometer). Het is vooral de UV-absorptie door ozon die de opwarming in de stratosfeer boven de tropopauze veroorzaakt.
Broeikasgassen vormen niet echt een hindernis voor de door de aarde uitgezonden warmtestraling, maar vertragen de energieoverdracht van de aarde naar de ruimte. Hoewel deze energieoverdracht kan worden vertraagd op weg naar de ruimte, uiteindelijk is er geen houden aan en zal de warmtestraling de ruimte in verdwijnen.
Bron: University of Colorado
Berekening thermisch evenwicht voor een aarde zonder atmosfeer:
De zon gedraagt zich ongeveer als een zwart lichaam met straal r s = 6,599 x 10 5 km, en een temperatuur van Ts = 5783 K. De stralingsflux van de zon aan het oppervlak wordt gegeven door de uitdrukking E=σTs^4, waarbij σ de Stefan -Boltzmann constante is (5,6704 x 10 -8 Wm2K4). Flux is de straling per oppervlakte-eenheid. De afstand aarde-zon is: res = 1,496 x 108 km. Daardoor vermindert de flux met een factor (rs / res)2. De aarde opgevat als schijf heeft een doorsnede cs = πr e2, waarin re de straal van de aarde is (6,378 x 103 km), dus onderschept de aarde cs σTs4 (rs / res)2 straling van de zon . Een evenwicht in de stralingsbalans tussen inkomende en uitgaande straling resulteert in een temperatuur Te, waarin σTe4 4πre2 = een cs σTs4 (rs / res)2. Dit leidt tot een temperatuur van de aarde Te = 272 K, dus -1 °C . Maar door wolken (natuurlijk alleen mogelijk als er een atmosfeer is) wordt ongeveer 30% van de invallende zonnestraling gereflecteerd. Als je hiermee rekening houdt kom je op een temperatuur van de aarde zonder atmosfeer van T e = 255 K, dus -18 °C . Als het aardoppervlak alleen gekoeld zou worden door uitstraling, dan zou de aarde ruim 60°C heet zijn. Dat is te warm voor veel leven op aarde. Maar door convectie van latente en voelbare warmte naar de hogere delen van de atmosfeer, en door grootschalige luchtcirculatie richting polen daalt de oppervlaktetemperatuur ruim 45 °C , en wordt de gemiddelde temperatuur van het aardoppervlak geschat op ongeveer 15 °C. Dat is dus de gemiddelde temperatuur als je het broeikaseffect mee rekent.
Overigens absorberen broeikasgassen niet alle langgolvige straling, maar slechts warmtestraling van bepaalde golflengtes en bandbreedtes. Bovendien zendt de aarde geen oneindige hoeveelheid warmte van de “juiste” golflengtes uit. Gevolg is dat er sprake is van competitie tussen de diverse broeikasgassen, zeker als ze werkzaam zijn op ongeveer dezelfde golflengtes, zoals CO2 en H2O.
Zo zouden wolken theoretisch wel 50% van de totale warmtestraling kunnen absorberen, maar in werkelijkheid is dat aanmerkelijk minder dan 50%. Voor de andere broeikasgassen geldt hetzelfde: de theoretisch maximaal haalbare absorptie van warmtestraling wordt nooit gehaald. Ondanks de aanwezigheid dus van broeikasgassen is de oppervlaktetemperatuur van onze aarde gemiddeld 15 °C in plaats van ruim 60 °C. Dit is het gevolg van convectie van warme lucht, waardoor grote hoeveelheden energie naar grotere hoogten worden getransporteerd en de uitstraling daar toeneemt. Bovendien speelt verdamping van water een rol, waardoor latente warmte tot bovenaan de troposfeer wordt getransporteerd.
Verandering is eigenlijk het enige constante kenmerk van het klimaat. Het wereldklimaat verandert voortdurend, zowel door invloeden vanuit de ruimte als op de aarde zelf. De Servische wiskundige Milutin Milanković onderzocht de oorzaken van de afwisseling van ijstijden en warme interglacialen gedurende de afgelopen 2,5 miljoen jaar. In de figuur hierboven is te zien dat er drie factoren zijn waardoor deze afwisseling verklaard kan worden: de excentriciteit van de aardbaan, de hoek van de aardas (obliquiteit) en het tollen van de aardas (precessie).
Maar ook andere buitenaardse factoren beïnvloeden het aardse klimaat, zoals de kracht van de zonne-energie, inslagen van grote meteorieten en fluctuaties in kosmische straling.
Er zijn naast “buitenaardse” factoren ook terrestrische klimaatfactoren werkzaam, zoals vulkanische activiteit, continentverschuivingen, en de ligging en aard van zeestromen.
Toch is de angst van de afgelopen tijd niet gericht op al deze bekende en soms krachtige klimaatfactoren, maar slechts op de toename van een van de broeikasgassen, namelijk CO2. Onder het versterkte broeikaseffect wordt dan verstaan de bijdrage die de door de mens veroorzaakte stijging van het CO2 -gehalte zou leveren aan de temperatuurstijging van de afgelopen eeuw. Het pre-industriële CO2 -gehalte van de atmosfeer wordt geschat op ongeveer 280 ppm, het huidige gehalte is 390 ppm.
 Bron: Kevin Trenberth
Bron: Kevin Trenberth
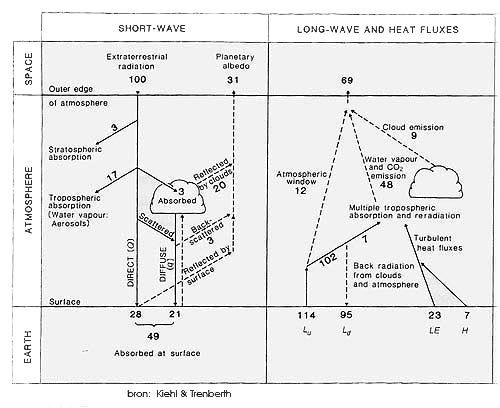
Bovenstaande figuur beeldt de klassieke stralingsbalans van de aarde uit. Ik noem deze “klassiek”, omdat deze balans al vele jaren het standaardmodel vormt van de energiestromen naar en van de aarde, en omdat er recent nieuwe hypothesen zijn geformuleerd waarin de stralingsbalans afwijkt van de standaardbalans. In deze en komende bijdragen poog ik enig inzicht te geven in de werking van de stralingsbalans en de invloed van broeikasgassen daarop.
Als men bovenstaande figuur nader bekijkt, dan is onmiddellijk te zien dat er inderdaad sprake is van een balans: what goes in must come out. Omdat het bij straling om energie gaat kunnen we die aangeven in Watt, dus per oppervlakte-eenheid Watt/m2 . Zonlicht (kortgolvige straling) is de bron van nagenoeg alle energie in de atmosfeer. De input van kortgolvige straling aan de buitenzijde van de atmosfeer is 341 Watt/m2. Daarvan verdwijnt 100 Watt/m2 doordat het licht reflecteert op wolken, op kleine deeltjes in de atmosfeer en aan het aardoppervlak (vooral op sneeuw- en ijsvelden). Wat overblijft wordt geabsorbeerd door het aardoppervlak (continenten en oceanen) en de atmosfeer. Dat is ongeveer 239 Watt/m2.
Door deze absorptie van kortgolvige straling warmt de aarde op en gaat langgolvige straling uitzenden (warmtestraling). De Eerste Wet van de Thermodynamica stelt dat energie niet verloren kan gaan, noch uit het niets kan ontstaan. Gevolg is dat de aarde net zoveel energie uitzendt als het ontvangt. Dus ook ongeveer 239 Watt/m2.
In onderstaande grafiek is de atmosfeer opgedeeld in 2 lagen, de troposfeer en de stratosfeer. De energiestromen van kortgolvige en langgolvige straling zijn in % aangegeven.
 Bron: John M.Wallace, Atmospheric Science.
Bron: John M.Wallace, Atmospheric Science.
Past men nu de Wet van Stefan-Bolzmann toe op deze 239 Watt/m2, dan is die 239 Watt/m2 de energie die een zwart lichaam uitstraalt met een oppervlaktetemperatuur zo’n -18 °C. In werkelijkheid is de oppervlaktetemperatuur ongeveer 15°C. Dit is de door metingen verkregen temperatuur. We gaan er van uit dat het verschil, 33°C, het gevolg is van het broeikaseffect, het effect dat broeikasgassen en wolken hebben op de temperatuur aan het aardoppervlak.
Maar als de aarde met een temperatuur van 15°C de ruimte in zou stralen in plaats van -18°C, dan zou de bijpassende energiestroom veel groter zijn dan 239 Watt/m2. En dat is onmogelijk volgens de Eerste Wet van de Thermodynamica. De aarde straalt gewoon 239 Watt/m2 de ruimte in , maar doet dat niet vanaf het warme aardoppervlak, maar vanaf grotere hoogte in de atmosfeer, waar de temperatuur veel lager is. Die afnemende temperatuur met de hoogte is het gevolg van het feit dat bepaalde gassen en wolken de langgolvige straling absorberen en weer uitzenden: het broeikaseffect. Overigens zou dit effect beter het atmosfeereffect kunnen heten, want de werking van een tuinderskas heeft veel meer te maken met het verhinderen van opstijgen van warme lucht dan van absorptie van langgolvige straling.
In bovenstaande figuur is te zien wat het broeikaseffect voor gevolgen heeft voor de temperatuur aan het aardoppervlak en de atmosfeer. De gestreepte lijn laat het effect zien indien er uitsluitend warmtestraling zou werken om warmtestraling de ruimte in te transporteren, dus de aarde af te koelen. Het zou aan het aardoppervlak een gemiddelde temperatuur van 60°C betekenen, een onleefbare temperatuur. Dat het broeikaseffect de aarde leefbaar maakt is dus erg betrekkelijk. Op de grens van troposfeer en stratosfeer zou de temperatuur onder deze omstandigheden ongeveer -85°C zijn.
De ononderbroken lijn laat de zogenaamde lapse rate zien, het werkelijk verloop van de temperatuur met de hoogte. Die lapse rate is gemiddeld -6.5°C/km. Het verschil zit in wat Spencer “weather” noemt. Het bestaat uit twee andere energiestromen die warmte van het aardoppervlak naar boven transporteren, namelijk voelbare warmte en latente warmte.
Die voelbare warmtestroom bestaat uit de verplaatsingen van warmte via luchtstromen, zowel vertikaal als horizontaal. De verticale luchtstromen brengen enorme hoeveelheden energie van het aardoppervlak naar grotere hoogte, waar broeikasgassen nauwelijks nog een rol spelen en er vrije uitstraling naar de ruimte kan plaatsvinden.
De latente warmtestroom is de energie die door verdamping in waterdamp meegevoerd wordt en op grotere hoogte weer vrijkomt bij condensatie. Het gevolg van beide processen is dat warmte van het aardoppervlak tamelijk efficiënt naar grotere hoogte wordt afgevoerd alwaar het door straling de ruimte in verdwijnt. Gevolg: de temperatuur aan het aardoppervlak daalt sterk, van gemiddeld 60°C naar 15°C: de aarde is leefbaar.
 Bron: Wallace & Hobbs, Atmospheric Science
Bron: Wallace & Hobbs, Atmospheric ScienceIn bovenstaande grafiek zijn beide lijnen uit de figuur van Spencer weer terug te vinden. De rode lijn is het gevolg van uitsluitend straling, de zwarte lijn is de lapse rate. De gestippelde lijn is de droogadiabaat, het temperatuurverloop als er uitsluitend warmte zou worden afgevoerd door droge stijgende luchtbellen, en er dus geen verdamping zou plaatsvinden.
Laten we even nader stilstaan bij deze uiterst belangrijke grafiek. Als een pakketje lucht wordt verwarmd, laten we zeggen boven een parkeerplaats op een zomerse dag, en het wordt warmer dan zijn omgeving, dan zet dat pakketje lucht uit, wordt lichter, en stijgt. Als dat pakketje verder stijgt komt het in luchtlagen waar de luchtdruk lager is dan voorheen en zet uit. Zie onderstaande grafiek.
 Bron: C. Donald Ahrens, Essentials in Meteorology
Bron: C. Donald Ahrens, Essentials in Meteorology
Daarbij daalt de temperatuur in het stijgende pakketje lucht adiabatisch met -9,8°C/km. Adiabatisch betekent dat er geen uitwisseling van warmte met de omgeving plaatsvindt. Uit de natuurkunde herkent u het getal 9,8 wel, dat te maken heeft met de zwaartekracht. De valversnelling of zwaarteveldsterkte is ongeveer 9,8, en bepaalt de drukverdeling in de atmosfeer zoals die in bovenstaande figuur is getekend. Zolang de temperatuur van de luchtbel hoger is dan van de omgeving zal het stijgen. Omdat de hoek van de droogadiabaat gemiddeld steiler is dan van de lapse rate zal de droogadiabaat op enige hoogte de lapse rate snijden: dit is de maximale stijghoogte (zie figuur hieronder). Op deze wijze wordt warmte van het aardoppervlak naar boven getransporteerd (voelbare warmte).
Veel belangrijker voor het warmtetransport is de nat-adiabaat, waarbij op enige hoogte waterdamp in de stijgende luchtbel condenseert vanwege de dalende temperatuur, waarbij de latente warmte die opgeslagen is in de waterdamp (dat is de warmte die nodig was om van water waterdamp te maken) weer vrij komt. Vanwege dat vrijkomen van de latente warmte zal de temperatuurlijn een knik vertonen (zie onderstaande grafiek). Door voordurende condensatie op weg naar boven zal er steeds meer warmte vrijkomen, waardoor de adiabaat op den duur een minder steil verloop krijgt, de lapse rate niet snijdt, en er zeer hoge wolken kunnen ontstaan.
Op dergelijke wijze wolken ontstaan die tot aan de grens van troposfeer en stratosfeer reiken, in de tropen is dat op ongeveer 17 km hoogte! In dergelijke tropische wolken die elke dag ontstaan over zeer grote oppervlakten gaan geweldige grote hoeveelheden warmte van het aardoppervlak de lucht in. Bedenk dat boven vrij verdampende wateroppervlakken zoals zeeën, oceanen en meren meer dan 90% van de afkoeling plaatsvindt via verdamping van water.
Maar ook boven land is verdamping van water de meest efficiënte vorm van afkoeling, vanwege evapotranspiratie, een samenvoeging van directe verdamping en verdamping via planten. Alleen in woestijnen, waar water nagenoeg ontbreekt, is afkoeling door verdamping geen optie, waardoor de temperatuur aan het aardopppervlak overdag zeer hoog op kan lopen. De warmte aan het aardoppervlak kan daar alleen door stijgende lucht (voelbare warmte) en ook een beetje door straling verdwijnen. Overigens is het wel zo dat het warmtetransport van latente warmte pas “afgerond ” is als regen uit de wolk het aardoppervlak bereikt.
Boven in de troposfeer raakt de lucht zijn warmte kwijt door uitstraling, nauwelijks meer geremd door broeikasgassen. De droge lucht wordt door windsystemen op grote hoogte getransporteerd en komt dan weer naar beneden. Tijdens het dalen wordt die relatief droge lucht adiabatisch opgewarmd en steeds droger en komt uiteindelijk onderin de troposfeer terecht, waar de hele cyclus weer van voor af aan begint.
Overigens zijn er behalve deze zeer sterke verticale luchtstromen in de tropen ook grootschalige verplaatsingen van voelbare en latente warmte in het horizontale vlak op aarde. Vanwege de zeer ongelijke verdeling van energie op aarde ontstaan er grootschalige windsystemen die warmte naar hogere breedten transporteren, en ook zeestromen zijn bij dit transport zeer belangrijk.
Op onze breedte ontstaan dan door botsing van warme vochtige lucht uit de tropen en koude lucht vanuit het poolgebied enorme wereldomspannende frontensystemen, waarbij langs die fronten en bijbehorende lagedrukgebieden sterk verticaal transport plaatsvindt met wolkvorming. Deze systemen brengen ook grote hoeveelheden warmte van het aardoppervlak naar de bovenkant van de troposfeer, alwaar de warmte door straling kan verdwijnen.
 Bron: C. Donald Ahrens, Essentials in Meteorology
Bron: C. Donald Ahrens, Essentials in Meteorology
Zoals ik al in deel 1 aangaf, is de latente warmtestroom verreweg de belangrijkste manier voor het aardoppervlak om warmte kwijt raken, gevolgd door voelbare warmtestromen. Het afkoelend effect van straling is gering, vergeleken met de latente en voelbare warmtestromen.
 Bron: Noor van Andel
Bron: Noor van Andel
Dr. Noor van Andel heeft enige tijd terug een heel aardige proef gedaan om dit aan te tonen. Hij heeft daartoe 7 schaaltjes buiten geplaatst, zoals op de figuur hierboven te zien is.
De schalen 1 en 2 zijn bedekt met 2mm kunststof PMMA, de een droog, de ander nat. PMMA (acrylaat) is een kunststof met de eigenschap dat het langgolvige straling tegenhoudt. De schalen 3 en 4 (ook droog en nat) zijn bedekt met een laagje (6 μm ) PE, polyetheen, dat langgolvige straling doorlaat. De schalen 4 en 5 zijn ook droog en nat, en beide open. Bakje 7 is open en heeft een aluminium spiegel aan de bovenzijde.
In alle bakjes is een thermokoppel geplaatst om nauwkeurig de temperatuur te kunnen meten. De bakjes zijn op een open grasveld voor het bedrijf van van Andel geplaatst, de meting startte op 9 mei 2008 om 21 uur en liep door tot de volgende dag 13 uur. Zowel de nacht als de volgende dag was het onbewolkt. Kijk eens naar de resultaten:
 Bron: Noor van Andel
Bron: Noor van Andel
‘s Nachts worden de schaaltjes met de PE bedekking het koudst: Pe laat de warmtestraling door, en de kunststof verhindert de lucht in het bakje om te mixen met de turbulente lucht erbuiten. Bakje 7 blijft het warmst, als gevolg van de vrije uitwisseling met de lucht en de spiegel die warmtestraling naar beneden reflecteert. Verder zijn er ’s nachts geen schokkende verschillen waarneembaar, het maximale temperatuurverschil is 10 °C.
Dat verandert de volgende dag sterk. De bakjes worden door de zon verwarmd. Het bakje met het IR-ondoorlatende PMMA wordt het warmst, meer dan 60 °C, terwijl het natte open bakje het koelst blijft, ongeveer 28 °C. Meer dan 30 °C verschil dus! Tussen de droge bakjes afgedekt met PMMA en PE is het verschil ongeveer 4 °C, dat is dus het effect van koeling door straling.
Verder zijn de verschillen tussen nat en droog bij alle 4 de afgesloten bakjes zichtbaar: bij PMMA ongeveer 6 °C, bij PE ongeveer 12 °C. Dat is het gevolg van verdamping van een deel van het water in de natte bakjes. Het sprongetje in de grafiek “PE droog” net voor 12 uur is waarschijnlijk het gevolg van het lekken van lucht naar buiten. Het verschil tussen “PE dry” en “open dry” is ongeveer 15 °C, en is het gevolg van het verhinderen van convectie (voelbare warmte) door de PE afdichting.
Al met al een toont dit eenvoudige proefje aan dat afkoeling door convectie (voelbare wamtestroom), maar vooral door verdamping (latente warmtestroom) veel efficiënter is dan door straling.
Bron: John M.Wallace, Atmospheric Science
Toch is er maar één mogelijke manier voor de atmosfeer om de “overtollige” warmte van de aarde definitief kwijt te raken , en dat is uitstraling naar de ruimte. Zoals reeds gezegd in deel 1 van dit onderwerp zou straling alléén dat nauwelijks aankunnen,met als gevolg dat de temperatuur aan het aardoppervlak tot gemiddeld 60 °C zou stijgen. Verticalen luchtstromingen in de troposfeer brengen echter grote hoeveelheden warmte (voelbaar en latent) naar de bovenkant van de troposfeer. Op die hoogte bevinden zich zo weinig broeikasgassen dat die warmte vrijwel ongehinderd uit kan stralen, zoals we verderop nog zullen zien. Dergelijke grootschalige convectiesystemen die grote hoeveelheden (latente en voelbare) warmte naar grote hoogten kunnen brengen bevinden zich onder andere in de tropen.
 Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Op bovenstaande figuur is te zien dat in de tropen een sterk afkoelend effect aanwezig is aan de bovenzijde van de troposfeer als gevolg van warmte-uitstraling. Die warmte is naar deze hoogte getransporteerd door reusachtige convectieve wolken die grote hoeveelheden warmte naar boven verplaatsen. Op onderstaande figuur zijn de grootste stromingen in de troposfeer weergegeven. Goed is te zien dat de lucht zich schijnbaar moeiteloos door de troposfeer beweegt. Verticale bewegingen zijn mogelijk doordat de temperatuuropbouw van de troposfeer die toelaat. Zie het stukje over de lapse rate in deel 1 van dit onderwerp.
 Bron: C. Donald Ahrens, Essentials in Meteorology
Bron: C. Donald Ahrens, Essentials in Meteorology
In de onderste 2 km van de troposfeer is de lucht zeer turbulent. Deze laag wordt de “atmospheric boundary layer” genoemd. Bewegingen boven deze laag uit ontstaan als gevolg van diepe convectie, waarbij door sterke opwarming, verdamping en wolkvorming de lucht tot aan de rand van de troposfeer kan stijgen. Verder gaat niet, in bovenstaande figuur is te zien waarom. In de stratosfeer neemt de temperatuur toe met de hoogte als gevolg van opwarming van het aanwezige O3. Deze inversie verhindert verdere stijging van lucht.
Aan de bovenzijde van de troposfeer vindt de feitelijke warmte-uitstraling plaats. Ruim 80% van de totale luchtmassa bevindt zich in de troposfeer. Vanaf ongeveer 10 km hoogte heeft het broeikasgas CO2 vanwege de sterke uitstraling van IR een afkoelende werking op de stratosfeer. Zie de grafiek hieronder.
 Bron: John M.Wallace, Atmospheric Science
Bron: John M.Wallace, Atmospheric Science
In tegenstelling tot CO2 is H2O niet in de gehele atmosfeer aanwezig maar vrijwel volledig in de troposfeer. In de grafiek is daarom de afkoelende werking van H2O in de stratosfeer veel kleiner dan CO2. Overigens begint de uitstraling van warmtestraling al vanaf 5 km hoogte; de lucht is daar al zo “dun” dat de warmtestraling al tamelijk makkelijk zijn weg naar de ruimte kan vinden.
 Bron: Whatsupwiththat
Bron: Whatsupwiththat
Broeikasgassen absorberen niet alle warmtestraling volledig, enkele stukjes met een beperkte bandbreedte kunnen, zonder geabsorbeerd te worden, uitstralen. In de figuur hierboven is dat goed te zien. Op de golflengte van ongeveer 10 μm wordt de warmtestraling nagenoeg niet geabsorbeerd door broeikasgassen en kan ongehinderd naar de ruimte verdwijnen. Dit is het zogenaamde atmosferische venster, dat in de stralingsbalans aangeduid wordt als Sr (atmospheric window). Die uitgaande energiestroom is ongeveer 40 Watt/m2 groot.
Op onderstaande figuur is te zien wat er met de absorptie van warmtestraling gebeurtop verschillende hoogten in de atmosfeer.
Langgolvige straling heeft een golflengte van 0,7 μm tot 300 μm. Het deel van de grafiek dat betrekking heeft op langgolvige (IR) straling is aan de bovenzijde aangegeven met een roze band. Het onderste deel van de grafiek is de absorptie van IR aan het aardoppervlak. Men ziet dat het grootste deel van de IR-band geabsorbeerd wordt door de broeikasgassen. Op 11 km hoogte echter (bovenzijde grafiek) is van die absorptie niet veel meer over dan een beperkt aantal zeer smalle bandjes. Het grootste deel van de warmtestraling kan op deze hoogte ongehinderd uitstralen.
Alle langgolvige straling verlaat ongehinderd de aarde en atmosfeer, met een energieniveau van 239 W/m^2, gelijk aan de gemiddelde geabsorbeerde kortgolvige straling. Dat komt, zoals we al zagen, overeen met een temperatuur van de aarde van 255 K ( -18 °C). Maar de atmosfeer is in werkelijkheid niet transparant voor langgolvige straling zoals we al zagen.
Van de figuur hierboven is onderstaande figuur afgeleid, met dien verstande dat nu goed te zien is in welk deel van het spectrum de langgolvige straling van de aarde vrijwel ongehinderd de ruimte in kan stralen. Het is het gebied met golflengten tussen 8 en 14 μm, het atmosferische venster genaamd. In de gebieden direct links en rechts van het atmosferisch venster is de atmosfeer ondoorzichtig voor langgolvige straling als gevolg van absorptie door broeikasgassen.
 Naar: http://www.theresilientearth.com
Naar: http://www.theresilientearth.com
Als de atmosfeer geen broeikasgassen zou bevatten dan kon langgolvige straling dus ongehinderd de aardse atmosfeer verlaten, en zou de gemiddelde temperatuur aan het aardoppervlak -18 °C zijn. De broeikasgassen zijn overigens niet gelijkmatig verdeeld in de atmosfeer. Alleen CO2 is tamelijk gelijkmatig verdeeld over de atmosfeer. Het belangrijkste broeikasgas, H2O, bevindt zich vooral in de troposfeer, daarboven neemt de hoeveelheid sterk af.
 Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Wat doen broeikasgassen met die langgolvige straling die van het aardoppervlak naar buiten wil? Die absorberen de langgolvige straling en emitteren die weer vrijwel onmiddellijk naar alle kanten. De langgolvige straling die naar de aarde gericht is vormt een deel van de Ed (back radiation) in de stralingsbalans van Trenberth. Het deel dat naar boven gericht is bereikt uiteindelijk de buitenzijde van de atmosfeer (TOA) waar het vrijelijk de ruimte in gaat (OLR in de stralingsbalans).
 Bron: University of Colorado
Bron: University of Colorado Als er op weg naar “boven” nog broeikasgasmoleculen aanwezig zijn zal de langgolvige straling nog een aantal malen geabsorbeerd en geëmitteerd worden. Voor langgolvige straling op pakweg 15 km hoogte is de atmosfeer daarboven vrijwel geheel doorzichtig. Voor langgolvige straling onder in de troposfeer is de weg naar buiten dus grotendeels opaak, ondoorzichtig.
Als uiteindelijk alle langgolvige straling de TOA bereikt, dus zowel de straling die ongehinderd de atmosfeer verlaat via het atmosferisch venster, als de langgolvige straling die moeizaam via absorptie en emissie de TOA bereikt, dan straalt daar gemiddeld 239 W/m^2 de ruimte in. En dat is exact gelijk aan wat er aan zonnestraling door de aarde geabsorbeerd wordt. Maar pas op: die 239 W/m^2 is een gemiddelde: vrijwel overal aan de buitenzijde van de atmosfeer is dat getal hoger of lager. Kijk alleen maar eens naar de onbalans als gevolg van de breedteligging die we in deel 1 al zagen:
 Bron: C. Donald Ahrens, Essentials in Meteorology
Bron: C. Donald Ahrens, Essentials in Meteorology
Maar ook het dag/nachtritme, de seizoenen en allerlei andere regionale en lokale effecten zorgen er voor dat er vrijwel nergens een stralingsbalans is tussen inkomende en uitgaande straling. Overigens is de inkomende zonnestraling ook vrijwel overal anders als gevolg van veelal dezelfde oorzaken als die voor langgolvige straling gelden. Die 239 W/m is dus een gemiddelde voor de gehele aarde op langere termijn bezien.
Op onderstaande figuur is de totale langgolvige straling afgebeeld in februari 2010, zoals die door de CERES satelliet is gemeten. Duidelijk is te zien dat er van globale uitstraling van 239 W/m^2 geen sprake is. De stralingsintensiteit is overal anders. Zou je de plaatjes van andere maanden ernaast leggen, dan zou je zien dat het niet alleen ruimtelijk bezien maar ook in de tijd voortdurend anders is.
 Bron: NASA
Bron: NASA
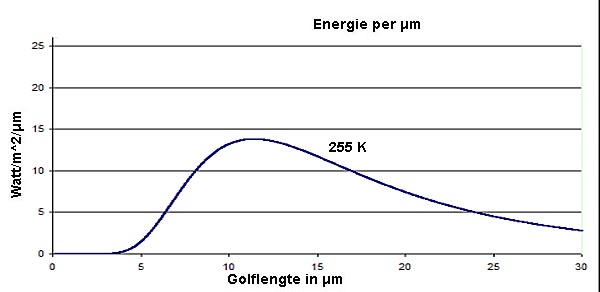
Bezien we nu onderstaande grafiek, dan zien we bovenin de weergave van 2 zogenaamde zwartlichaam spectra volgens de Wet van Planck. De linker is van de zon, maar we zijn hier meer geïnteresseerd in de rechter kromme, die van de langgolvige straling van een zwart lichaam bij 255 K ( = -18 °C). De aarde is niet volledig een zwart lichaam, maar benadert die toch sterk.
 Bron: John M.Wallace, Atmospheric Science
Bron: John M.Wallace, Atmospheric Science
Bovenstaande grafiek is het theoretisch spectrum van de langgolvige straling van de aarde. Hoe het er in werkelijkheid uitziet weten we onder andere dank zij de Nimbus 4 satelliet die uitgerust is met een zogenaamde infrared interferometer spectrometer. Het energiespectrum wijkt qua vorm af van de figuur hierboven, maar dat is het gevolg van het feit dat de horizontale as van de bovenste figuur logaritmisch verloopt, terwijl dezelfde as op de figuur hieronder een lineaire schaal heeft.
 Naar: K.N.Liou, An Introduction to Atmospheric Radiation
Naar: K.N.Liou, An Introduction to Atmospheric Radiation
In de figuur zijn afgebeeld de spectra bij diverse temperaturen. Met rood is het spectrum aangegeven van een lichaam met een temperatuur van 255 K, -18 °C, de aarde dus. De grillige lijn is de gemeten langgolvige straling die vanaf de aarde ruimte in gaat.
Tussen de 8 en 14 μm heeft het uitgezonden spectrum een profiel dat in de buurt ligt van 290 K. Dit is de langgolvige straling die rechtstreeks via het atmosferisch venster de ruimte in gaat. Die 290 K komt globaal overeen met de gemiddelde temperatuur aan het aardoppervlak, namelijk 15 °C ( 288 K). Het kleine dipje bij 10 μm is het gevolg van absorptie door O3.
Tussen de 14 en 18 μm is het energieniveau zo laag dat het past bij het profiel van 220 K , -53 °C. Dat is de temperatuur aan de bovenzijde van de troposfeer op ongeveer 11 km hoogte. Oorzaak hier is de sterke absorptie in deze band door CO2, waardoor pas op grote hoogte , waar het koud is, uitstraling naar de ruimte plaats kan vinden.
Tussen 5 en 8 μm vindt uitstraling ook op een kouder niveau plaats, namelijk tussen ongeveer 0 °C en -50 °C, als gevolg van de absorptie van H2O in deze band. Op onderstaande figuur is een en ander duidelijk te zien:
 Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Bron: K.N.Liou, An Introduction to Atmospheric Radiation
Vereenvoudigd kunnen we dus het volgende stellen: de atmosfeer raakt op 2 manieren haar warmtestraling kwijt, namelijk voor de golflengtes tussen 8 en 14 μm door directe uitstraling via het atmosferisch venster, en voor de andere golflengtes via absorptie en emissie van broeikasgassen en tenslotte via uitstraling aan de TOA.
Stel nu eens dat de atmosfeer voor 100% transparant zou zijn voor langgolvige straling, dan zou het energiespectrum er zo uit zien:
Stel nu dat de atmosfeer wel het atmosferisch venster heeft , maar dat het voor de banden daarbuiten 100% opaak (ondoorzichtig) is. Hoe zou het spectrum er dan uit zien? Dat zou betekenen dat de aarde haar warmte alleen door het relatief smalle venster van 8 tot 14 μm kwijt kan raken. Om dat mogelijk te maken zal de temperatuur van het aardoppervlak flink omhoog moeten, wel tot zo’n 50 °C. Waarom is dat logisch?
Let eens op de verticale as van bovenstaande grafiek. De eenheid is W/^2/ μm. Dat betekent dat voor elke band van 1 μm breed in de grafiek afgelezen kan worden hoeveel W/m^2 uitgestraald wordt op TOA niveau, voor een lichaam met een temperatuur van -18 °C. De totale oppervlakte van de kromme geeft dus de totale hoeveelheid uitgestraalde energie weer over alle banden. Maak ik de breedte van die oppervlakte smaller, dan moet, om dezelfde hoeveelheid energie uit te kunnen stralen, de energie-inhoud per 1 μm-bandje omhoog, en daarmee de grafiek. En bij een hogere grafiek hoort een hogere temperatuur van het uitstralende object. De buitenzijde van de aarde wordt om dit mogelijk te maken, “vanzelf” meer dan 50 °C. Zie de grafiek hieronder.

Vanzelfsprekend wijkt de werkelijkheid af van bovenstaand gedachte-experiment. Immers, voor de banden buiten het atmosferisch venster is de atmosfeer niet volledig ondoorzichtig. En die transparantie neemt toe met de hoogte: immers, de dichtheid van de atmosfeer neemt sterk af naarmate men hoger komt. Op ruim 5 km hoogte is de luchtdruk nog maar de helft van die aan het aardoppervlak, op 10 km hoogte is de luchtdruk nog maar 1/5 van die aan het aardoppervlak. Voor langgolvige straling die buiten het atmosferisch venster wil ontsnappen betekent dat de transparantie op 5 km hoogte 2x zo groot is als aan het aardoppervlak. Op 15 km hoogte zijn er nog weinig broeikasgasmoleculen die een ongehinderde uitstraling naar de ruimte belemmeren.
Voor het uitstralen van warmte naar de ruimte, de enige manier voor de aarde om uiteindelijk warmte kwijt te raken, zijn dus grofweg de onderste 15 km van de atmosfeer van belang. Elke “laag” in de troposfeer heeft dus zijn “eigen” transparantie voor wat betreft uitstraling naar boven. Hoe hoger je komt des te makkelijker dat gaat. Let wel: de temperatuur neemt met de hoogte af met gemiddeld -6,5 °C, de lapse rate. De gevolgen daarvan zullen we verderop nog zien.
Bron: John M.Wallace, Atmospheric Science
Om te begrijpen wat broeikasgassen doen is het dus noodzakelijk om de atmosfeer niet als 1 laag te beschouwen, maar uit een (schier oneindig) aantal laagjes. Maar om te begrijpen wat er gebeurt in die vele laagjes is een beetje lastig, dus is het verstandig om net te doen alsof de atmosfeer maar uit enkele lagen bestaat, zeg 4 lagen. Wat gebeurt er nu in die 4 lagen met de langgolvige warmtestraling die van de aarde komt?
In onderstaande tekening is dat modelmatig weergegeven. Het betreft de naar buiten gerichte stroom langgolvige straling buiten het atmosferisch venster. Let op: dit is een sterk vereenvoudigde weergave van de werkelijkheid. De gebruikte waarden zijn fictief. Alleen opwaartse langgolvige straling is weergegeven. Zoals te zien is, is de transparantie voor langgolvige straling beter hoger naarmate de uitstralende laag zich hoger in de atmosfeer bevindt. Anders gezegd: de opaciteit van de atmosfeer is het grootst nabij het aardoppervlak. Dat is het gevolg van het feit dat de atmosfeer dunner wordt naarmate je hoger komt, en ook omdat er relatief minder broeikasgassen zijn op grotere hoogte.
In ons voorbeeld bereikt 7 + 11 + 25 + 48 = 91 W/m^2 via de atmosfeer (buiten het atmosferisch venster) de TOA, waar het vrij de ruimte in straalt. In werkelijkheid is dit getal hoger. Immers, bij de TOA is de gemiddelde uitstraling 239 W/m^2. Als je daar de 40 W/m^ (stralingsbalans Trenberth) van aftrekt, straalt de atmosfeer dus 199 W/m^2 uit. Zoals ik al zei, de gebruikte getallen zijn fictief, en die 4 lagen zijn er in werkelijkheid schier oneindig veel. In ons model is te zien dat de emissie van langgolvige straling naar de ruimte dus op allerlei niveaus plaats vindt. Relatief weinig (maar met een hoge temperatuur) vanaf de lagen direct boven het aardoppervlak, en veel maar bij lagere temperaturen hoger in de troposfeer. Het “gemiddeld” emissieniveau ligt op 5km hoogte, waar de temperatuur -18 °C is.
Volgens de Wet van Stefan-Boltzmann komt dat overeen met 239 W/m^2. Die Wet (of vergelijking) luidt E = σT4 . In deze vergelijking is E de uitgestraalde energie, σ een constante (5.67 x 10^-8) en T is de temperatuur in Kelvin. Hier moet wel bij aangetekend worden dat het feitelijk onmogelijk is om het “gemiddeld emissieniveau ” te bepalen. Je kunt dus stellen dat men, terug rekenend van 239 W/m^2 en gebruik makend van Stefan-Boltzmann, men uitkomt op -18 °C en de bij deze temperatuur horende hoogte, 5 km, het “gemiddeld emissieniveau” noemt. Doordat de temperatuur in de troposfeer afneemt met de hoogte zullen hogere (=koudere) lagen vanwege hun lagere temperatuur minder makkelijk energie uitstralen naar boven dan van onderen absorberen.
Wat gebeurt er nu als er bijvoorbeeld meer langgolvige straling absorberende stoffen in de atmosfeer komen, zoals bijvoorbeeld CO2 ? Dan neemt de transparantie af ( dus de opaciteit toe) , en dat geldt voor elke laag in het model. Alleen het atmosferisch venter heeft nergens last van. Maar buiten het atmosferisch venster zal de uitstraling uiteindelijk minder worden. Stel dat de transparantie met 10% afneemt, dan daalt in bovenstaande model van 92 W/m^2 naar ongeveer 82 W/m^2.
Wat betekent dit nu voor de diverse lagen in de atmosfeer? Alle lagen worden door een toename van broeikasgassen minder transparant. Voor de lagen direct boven het aardoppervlak betekent dit dat de transparantie tot bijna 0 wordt teruggebracht. De lagen daarboven krijgen ook ‘last’ van verminderde transparantie. Alleen de TOA aan de bovenzijde kan nog steeds vrijelijk uitstralen. Uiteindelijk bereikt de langgolvige straling die vanaf het aardoppervlak uitgestraald wordt wel de TOA, maar er zijn onderweg meer broeikasgasmoleculen die de straling kunnen absorberen en naar alle kanten emitteren. Het gevolg hiervan is dat de onderste laag van de troposfeer nauwelijks nog in staat is om straling direct de ruimte in te zenden.
Hoe werkt dat? Laten we nog eens terug gaan naar het model. In het model is de transparantie van de laag op 5 km hoogte (fictief) gesteld op 3%. Dat betekent dat slechts 3% van de langgolvige straling die deze laag naar boven emitteert, zonder onderweg geabsorbeerd te worden de TOA bereikt en uitstraalt naar de ruimte. Dus 97% van de straling uit die laag wordt op een of andere hoogte bovenin geabsorbeerd en geëmitteerd. Neemt nu de transparantie van de atmosfeer met 10% af als gevolg van een toename van broeikasgassen, dan kan nog slechts 2,7% ongehinderd de TOA bereiken. De rest, 97,3% bereikt via de bovenliggende lagen (absorptie en emissie) de TOA. De laag op 5 km straalt dus minder langgolvige straling direct uit. Let op: dit is de laag met een relatief hoge temperatuur die relatief veel energie emitteert. De rest van de langgolvige straling uit die onderste laag wordt geabsorbeerd en geëmitteerd door hoger liggende lagen, die elk vanwege de toename van het broeikaseffect ook 10% minder direct naar de TOA kunnen uitstralen. Alleen de allerhoogste laag, de TOA, heeft geen last van toegenomen broeikasgassen en emitteert alle resterende langgolvige straling de ruimte in.
Wat zijn de gevolgen? Dat de lagen onderin de troposfeer (de warmere lagen) minder uitstralen, en bijgevolg de hogere (koudere) relatief meer. Als je aan die langgolvige straling meet die vanaf de TOA de ruimte ingaat, en je meet de zogenaamde “brightness temperature”, dan zul je dus een gemiddeld lagere temperatuur meten. Maar belangrijker is dat bij een lagere temperatuur een lagere energiestroom hoort. De energiestroom die de aarde verlaat wordt minder dan 239 W/m^2: de stralingsbalans is uit balans. En bij een lagere temperatuur hoort volgens Stefan-Boltzmann een energiestroom die dus ook kleiner is dan 239 W/m^2. Gevolg: het “gemiddeld emissieniveau” schuift wat naar boven , naar een koudere laag.
 Bron: John M.Wallace, Atmospheric Science
Bron: John M.Wallace, Atmospheric Science
Het model hierboven is echter een sterk vereenvoudigde weergave van de werkelijkheid. In werkelijkheid neemt de transparantie alleen af bij die golflengten waarin het broeikasgas actief is. Kijken we nog eens naar bovenstaande figuur die we al eerder tegenkwamen. In de band tussen 5 en 8 μm wordt in de onderste laag de langgolvige straling voor 100% geabsorbeerd door H2O. Op 11 km hoogte is die absorptieband geslonken tot het gebied tussen ongeveer 6 en 7 μm, en de absorptie is tot ongeveer 50% geslonken. Op deze hoogte zijn nog maar 2 smalle bandjes waar de absorptie 100% is, namelijk nabij 4 μm en 15 μm.
Bij een verhoging van het CO2-gehalte zal het volgende gebeuren: de banden die nog niet opaak zijn zullen minder transparant worden. Dat geldt voor elke laag op elke hoogte in de atmosfeer. De onderste lagen hebben relatief veel banden die 100% opaak zijn. Een verhoging daarvan is niet mogelijk. Maar wat wel gebeurt is dat de banden direct grenzend aan een dergelijke “verzadigde band” nog wel hun opaciteit zien toenemen, zoals op bovenstaand figuur geschetst is. In de hogere lagen komen meer banden voor die slechts gedeeltelijk opaak zijn. Daar zal bij een verhoging van het CO2-gehalte dit gebeuren:
Op onderstaande figuur is te zien binnen welke banden elk van de broeikasgassen actief is:
De gangbare hypothese is nu dat het aardse systeem de stralingsbalans zal herstellen door de temperatuur in het onderste deel van de atmosfeer wat te verhogen: het versterkt broeikaseffect. Er is immers sprake van een input (netto inkomende kortgolvige straling) die iets groter is dan de output (netto uitgaande langgolvige straling). Door die toename van de temperatuur zal de temperatuur aan het aardoppervlak iets hoger worden. Bij een verdubbeling van het CO2-gehalte zal dat een temperatuurstijging betekenen van iets meer dan 1 °C . Dat wil zeggen: ALS ALLE ANDERE ZAKEN IN HET KLIMAATSYSTEEM GELIJK BLIJVEN.
In de stratosfeer gebeurt het tegenovergestelde: als het broeikaseffect toeneemt, dan neemt de temperatuur af. Hoe is dat verklaarbaar? We zagen hiervoor al dat CO2 in de stratosfeer een sterk afkoelend effect heeft. In onderstaande grafiek is te zien dat de temperatuur – anders dan in de troposfeer – in de stratosfeer toeneemt met de hoogte. Dat is het gevolg van het feit dat de in de stratosfeer aanwezige O3 vrijwel alle uv-straling uit het zonlicht absorbeert. Volgens de Wet van Stefan-Boltzmann betekent dit dat hogerliggende lagen in de stratosfeer vanwege hun hogere temperatuur makkelijker ( lees: meer) energie naar de ruimte stralen dan aan de onderzijde absorberen.
 Bron: C. Donald Ahrens, Essentials in Meteorology
Bron: C. Donald Ahrens, Essentials in Meteorology
De stralingsbalans onder vuur.
Er is het een en ander aan te merken op de ‘klassieke’ stralingsbalans en daarmee op de broeikastheorie die ik de afgelopen weken op deze site uit de doeken heb gedaan. Die stralingsbalans van de wetenschapper Trenberth staat hieronder nogmaals afgebeeld. Deze stralingsbalans vormt de basis voor een stroom van artikelen over het broeikaseffect, en ook voor de laatste twee rapporten van het IPCC, het derde en het vierde rapport. Ik ga de komende tijd proberen gefundeerde kritiek op een rijtje te zetten. In dit eerste deel staat de input van de stralingsbalans van Trenberth centraal, namelijk de inkomende zonnestraling.
 Bron: Trenberth
Bron: Trenberth
De klassiek opvatting is als volgt: De zonneconstante is 1366 W/m^2. Hieraan hoeft niet getwijfeld te worden. Dat betekent dat op een vlak dat loodrecht staat op de zonnestraling en zich op dezelfde afstand van de zon bevindt als de aarde, per vierkante meter 1366 Watt aan stralingsenergie valt. Die 1366 W/m^2 is overigens niet zo constant als de naam doet vermoeden: lichte schommelingen met een periodiciteit van 10 a 11 jaar zijn normaal, zoals onderstaande figuur toont.
 ron: Wikipedia
ron: Wikipedia
Vanwege de excentriciteit van de baan van de aarde rond de zon met een periodiciteit van 100. 000 jaar (zie Milanković in het hoofdstuk onder De Feiten) schommelt de zonneconstante op enig moment, namelijk van 1412 W/m² in januari tot 1312 W/m² in juli. Voor ons doel, de stralingsbalans op dit moment, kunnen we uitgaan van 1366 W/m^2 zonder grote fouten te maken.
Deze zonneconstante is, zoals ik al schreef, de hoeveelheid energie op een plat vlak. In werkelijkheid is de aarde geen plat vlak , maar een bol. Wat voor consequenties dat heeft is duidelijk: een bol heeft een 4x zo grote oppervlakte als een schijf met dezelfde straal. De oppervlakte van een ronde schijf met straal r is immers ᴫr^2, die van een bol is 4 ᴫr^2.
Bron: Slaying the Sky Dragon
Rekenkundig bezien valt er daarom gemiddeld op elke m^2 op de bol die aarde heet dus 1366/4 = 341,5 W. Herkent u dat laatste getal? Juist het is de (afgeronde) 341 W/m^2 die in de stralingsbalans van Trenberth de input vormt aan de buitenzijde van de atmosfeer.
Wil men nu uit deze 341 W/m^2 de gemiddelde temperatuur op aarde berekenen, dan is het wel nodig om rekening te houden met het deel van het zonlicht dat reflecteert en dus de aarde niet kan verwarmen. De albedo is ongeveer 0,3. Dus 0,7 x 341 = 239 W/m^2. Men gaat bij deze berekeningen er altijd van uit dat de aarde een zwart lichaam is. Met behulp van de Stefan-Bolzmannvergelijking is nu de gemiddeld maximale temperatuur te berekenen: K^4= 239/ 5,67 x 10 ^-8, en dat wordt 255 K. Dat is dus die -18 °C zonder broeikasgassen.
Tot zo ver niets aan de hand, lijkt het. Maar zo simpel is het in werkelijkheid niet. Want aan het berekeningentje hierboven is al te zien dat tussen de temperatuur in K en de toegevoerde energie geen lineair verband bestaat maar een verband met een vierde macht. Met andere woorden: als er Y hoeveelheid stralingsenergie nodig is om een object een temperatuur K te geven, dan is 16 maal Y nodig om datzelfde object een temperatuur 2K te geven! En dat heeft gevolgen voor de opwarming van de aarde.
In het intrigerende e-book “Slaying the Sky Dragon” dat onlangs is verschenen en dat al veel stof heeft doen opwaaien, wordt deze kwestie van de inkomende straling uitgebreid behandeld.
Om in te kunnen zien wat het verschil is tussen de theoretisch-wiskundige berekening van de inkomende energie en de werkelijkheid doen we een gedachte-experiment. Stel dat de warmtecapaciteit van de aarde 0 is, en de warmtegeleidbaarheid ook. En dat de aarde heel langzaam rond zijn as draait. Dan zou de temperatuur aan het aardoppervlak gedurende 2 omwentelingen het volgende verloop kennen:
 Bron: A Greenhouse Effect on the Moon?
Bron: A Greenhouse Effect on the Moon?
De verklaring hiervoor is de volgende: slechts de halve bol vangt het zonlicht op, de andere helft is in duisternis gehuld. Indien de aarde een schijf zou zijn , dan valt er op de gehele schijf 1366 W/m^2. Met behulp van de Stefan-Bolzmannvergelijking, kan men de geabsorbeerde stralingsenergie van een zwart lichaam omrekenen naar temperatuur. Dat levert een maximale temperatuur op van (1366 /5,67)^0,25 x 100 = 394 K . Die 394 K zal overal op de schijf aanwezig zijn, dus de maximale temperatuur is meteen de gemiddelde temperatuur.
Maar bij een bol werkt dit anders. De verlichte helft heeft een oppervlak van 2 ᴫr^2, dus er valt aan de buitenzijde van de atmosfeer op 1 m^2 gemiddeld 1366/2 = 683 W/m^2. Omgerekend naar de gemiddelde maximale temperatuur levert dat op: (683/ 5,67)^0,25 x 100 , een temperatuur van 331 K. Dat is de gemiddelde temperatuur van de verlichte helft. Omdat de halve bol sferisch is, is er maar 1 plek waar het zonlicht loodrecht invalt. Daar vangt de halve bol dus de maximale hoeveelheid stralingsenergie en wordt de temperatuur maximaal ( 394 K) op alle andere plekken op de verlichte helft is dat minder en loopt dat terug tot 3 K op de grens van licht en donker. Dit komt exact overeen met de cijfers uit een rapport van de NASA, “An Analysis and Procedure for Determining Space Environmental Sink Temperatures With Selected Computational Results”.
De achterzijde van de bol ontvangt 0 W/m^2, en heeft dus een temperatuur van 0 K. In werkelijkheid kan de temperatuur aan de schaduwzijde niet verder dalen dan de zogenaamde achtergrondstraling van het helaal, die is ongeveer 3 K. Gemiddeld voor de hele bol is dat dus 331 + 3 = 334/2 = 167 K. Vergelijk dat eens met de 255 K van de stralingsbalans.
NASA heeft theoretische berekeningen gemaakt van de temperaturen op de maan, en ze ook kunnen vergelijken met de meetgegevens door de satelliet Diviner. Nu wijken de voorspelde temperaturen op de maan behoorlijk af van de theoretisch berekende, zoals hierboven beschreven. Zo zorgt de opslag van warmte in de maan er voor dat een deel van de stralingsenergie die op het verlichte deel valt niet direct wordt omgezet in een (hoge) oppervlaktetemperatuur, maar gebruikt wordt om de maan op te warmen. Er ontstaat dus een buffer van warmte. Dat bufferen van warmte zorgt er voor dat de maximale temperatuur lager zal zijn dan 394 K, en ook de gemiddelde temperatuur lager zal zijn dan 331 K.
Bron: A Greenhouse Effect on the Moon?
Aan de andere kant zorgt de gebufferde warmte er voor dat aan de schaduwkant de afkoeling langzaam plaats vindt, en de theoretische 3 K bij lange na niet bereikt wordt. Voordat de donkere zijde kan afkoelen tot 3 K is de maannacht (ongeveer 2 weken) al weer voorbij en warmt het oppervlak op. Op boventaande figuur is het berekende verloop weergegeven met de blauwe lijn. De rode lijn is de gemeten temperatuur aan het maanoppervlak.
Er valt op dat het warmste punt van de (maan-)dag zich niet bevind als de zon het hoogst aan de maanhemel staat , maar later in de maanmiddag. Zo is dat op aarde ook. Zoals te zien is wijkt de gemeten temperatuur af van de berekende, onder andere vanwege de afwijkende warmtegeleidbaarheid van de maan. Op het verlichte deel is de gemeten temperatuur wat lager dan de berekende. Overigens is de maximaal berekende temperatuur iets lager dan de hiervoor al berekende 394 K, omdat rekening gehouden is met de albedo van de maan van 0,11. De laagste gemeten temperaturen op de maan vallen opmerkelijk hoger uit dan de berekende. Oorzaak is de warmtestraling van de aarde. De gemeten temperatuur op de maan valt in het verlichte deel 20 K lager uit dan berekend, en in het donkere deel zelfs 40 K hoger!
De metingen aan de maantemperatuur worden verricht door de Diviner Lunar Radiometer, een van de 7 meetinstrumenten aan boord van NASA’s Lunar Reconnaissance Orbiter. Hieronder zijn impressies afgebeeld van de gemeten temperatuur aan de verlichte en donkere zijde van de maan.
Bron: UCLA
We zagen hiervoor al wat de theoretische maximum en gemiddelde temperaturen van de aarde zijn. Rekening houdend met de aardse albedo van 0,3 levert dat een maximale temperatuur op van ((1366 X 0,7)/5,67)^0,25 x 100 = 360 K . Voor de aarde als bol wordt de gemiddelde temperatuur van het verlichte deel: ((1366/2)/ 5.67×0,7))^0,25 x 100 = 303 K. De achterzijde wordt 3 K . De gemiddelde temperatuur van de gehele bol is dus 303 + 3= 306/2= 153 K.
De werkelijke aarde slaat energie op in water en land, en staat dat ook weer langzaam af. Warmtecapaciteit, warmtegeleiding en oceaanstroming bepalen dan samen met de omloopsnelheid van de aarde hoe het temperatuurverloop er uit gaat zien. De aarde draait met een pittige snelheid (in 24 uur) een keer rond zijn as, waardoor de opwarming niet maximaal wordt en de afkoeling bij een relatief hoge temperatuur blijft steken. Bovendien bestaat het aardoppervlak voor 70% uit water, dat een enorme buffercapaciteit heeft voor warmte. De buffercapaciteit van de aarde is vele malen groter dan die van de maan met zijn stenige oppervlak.
Onderstaande figuur geeft een impressie wat dit voor gevolgen kan hebben voor het verloop van de temperatuur op aarde. Vanwege de enorme buffercapaciteit van met name de oceanen zal de blauwe lijn in werkelijkheid een veel vlakker verloop hebben dan weergegeven.
Bron: Slaying the Sky Dragon
Conclusies: de berekening van de gemiddelde temperatuur op aarde is op basis van de eenvoudige berekening zonneconstante/4 : 1366/4= 341,5 W/m^2 . Rekening houdend met de albedo van 0,3 krijgt men dan: 341,5 x 0,7 = 239 W/m^2. Dit is het getal dat aan de basis staat van de stralingsbalans van Trenberth, die al meer dan 10 jaar als uitgangspunt genomen wordt als het om de energiestromen van de aarde gaat.
Op basis van hetgeen hiervoor is beschreven mag geconcludeerd worden dat deze berekening onjuist is. Belangrijkste oorzaak daarvan is dat de aarde altijd een verlichte en een donkere zijde heeft, en dat het verband tussen energie en temperatuur niet lineair is maar met een vierde macht verloopt. Bovendien wijzen metingen aan de maan erop , dat er nog meer complicerende factoren zijn waardoor het uiteindelijke temperatuurverloop anders is dan de theoretisch berekende.
Het wordt nog merkwaardiger als men bedenkt dat de output van Trenberth’s stralingsbalans “kloppend” gemaakt is op basis van de verkeerde input. En dat de hiervoor uitgebreid beschreven broeikastheorie er van uitgaat dat een eventuele onbalans tussen de inkomende zonnestraling (input) en de uitgaande warmtestraling (output) als gevolg van een toenemend CO2-gehalte gecorrigeerd wordt door een stijging van de oppervlaktetemperatuur. Met recht mag men hier vragen: over welke input en output gaat het hier?


























