In het rapport van Crok en Lewis dat onlangs uitgebracht is (zie het bericht van 6 maart j.l.) wordt de klimaatgevoeligheid van het klimaatsysteem bekeken op basis van observationele gegevens, de nieuwste inzichten in gedrag van aerosolen  en met behulp van hoogwaardige  statistische methodiek. Daarbij komen de schrijvers tot een opmerkelijk lagere klimaatgevoeligheid dan tot nu toe door het IPCC werd aangenomen. De mondiale klimaatmodellen die door het IPCC gebruikt worden om toekomstige klimaatverandering te voorspellen genereren een klimaatgevoeligheid tussen de 2°C en 4,5°C,met een gemiddelde van net boven de 3°C.

Het begrip klimaatgevoeligheid is om diverse redenen een lastig begrip. Het betreft de respons van het klimaatsysteem , geschat voor de temperatuur aan het aardoppervlak, bij een verdubbeling van het broeikasgas CO2. Een dergelijke respons heeft tijd nodig omdat het klimaatsysteem traag reageert. Dat is is vooral het gevolg van het enorme bufferende vermogen van de oceanen. We gaan er van uit dat na enkele eeuwen zich een nieuw evenwicht heeft ingesteld, het ECS (equilibrium climate sensitivity). Bekijkt men het temperatuureffect van CO2-verdubbeling over een periode van 70 jaar dan spreekt men van TCR (transient climate sensitivity).

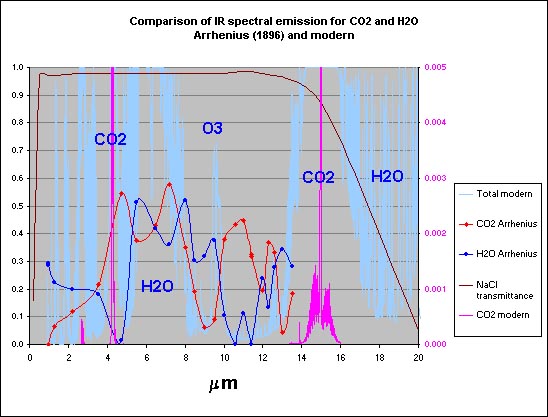
De eerste wetenschapper die de klimaatgevoeligheid probeerde te berekenen was de zweed Svante Arrhenius. (  Svante Arrhenius, 1896, On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science [fifth series] April 1896. vol 41, p237-275 ).  Hij kwam op een klimaatgevoeligheid van 4 tot 6 °C.  Alhoewel Arrhenius nog steeds gezien wordt als de grondlegger van de broeikastheorie moet toch wel gezegd worden dat zijn berekeningen onjuist waren. Ze waren gebaseerd op het verkeerde IR-spectrum. Hans Erren heeft een aantal jaren geleden hierover een aardig stuk geschreven.

Bron: Hans Erren

Vanaf 1979 is geprobeerd om de klimaatgevoeligheid te schatten aan de hand van klimaatmodellen. De eerste schatting was gebaseerd op twee in moderne opzichten rudimentaire klimaatmodellen. De een kwam uit op een ECS van 2 °C, de andere op 4 °C. Beste schatting werd 3 °C.  En merkwaardig genoeg, ondanks voortschrijdend wetenschappelijk inzicht en het inzetten van geavanceerde gekoppelde oceaan-atmosfeermodellen, is die beste schatting tot op heden 3 °C gebleven. Van der Sluijs verklaart dat omdat een “noodzakelijke solide basis nodig was voor klimaatbeleid”. Waarbij we meteen met de neus op de feiten gedrukt worden: klimaatgevoeligheid is een politiek instrument geworden.

Er is ook een andere methode dan het gebruik van modellen om de klimaatgevoeligheid te schatten, en dat is door observaties. Op deze site is al vaak stil gestaan bij de energiebalans van de aarde. Voor die balans geldt: what comes in must go out.  Wel natuurlijk even rekening houden met het bufferend vermogen van vooral de oceanen natuurlijk.

De methode is echter wel afhankelijk van betrouwbare schattingen van:

• veranderingen in de mondiale stralingsforcering. Stralingsforcering is de onbalans die kan ontstaan als er meer energie het systeem binnenkomt dan uitgaat.
• stralingsonbalans bovenin de atmosfeer (TOA) (of diens tegenhanger, de warmteopname van het klimaatsysteem, voornamelijk de oceanen)
• de mondiale temperatuur aan het oppervlak.

Bron: Trenberth

De theorie is dat door een stijging van het CO2-gehalte een positieve stralingsforcering ontstaat doordat de atmosfeer meer opaak wordt voor ir-straling.  De warmtestraling kan  als het ware minder makkelijk het systeem verlaten waardoor de temperatuur aan de onderzijde van de atmosfeer stijgt.

Om te begrijpen wat broeikasgassen doen is het noodzakelijk om de atmosfeer niet als 1 laag te beschouwen, maar uit een (schier oneindig) aantal laagjes.  Maar om te begrijpen wat er gebeurt in die vele laagjes is een beetje lastig, dus is het verstandig om net te doen alsof de atmosfeer maar uit enkele lagen bestaat, zeg 4 lagen. Wat gebeurt er nu in die 4 lagen met de langgolvige warmtestraling die van de aarde komt?

In onderstaande tekening is dat modelmatig weergegeven. Het betreft de naar buiten gerichte stroom langgolvige straling buiten het atmosferisch venster.  Let op: dit is een sterk vereenvoudigde weergave van de werkelijkheid. De gebruikte waarden zijn fictief. Alleen opwaartse langgolvige straling is weergegeven. Zoals te zien is, is de transparantie voor langgolvige straling beter hoger naarmate de uitstralende laag zich hoger in de atmosfeer bevindt. Anders gezegd: de opaciteit van de atmosfeer is het grootst nabij het aardoppervlak. Dat is het gevolg van het feit dat de atmosfeer dunner wordt naarmate je hoger komt, en ook omdat er relatief minder broeikasgassen zijn op grotere hoogte.

In mijn voorbeeld bereikt 7 + 11 + 25 + 48 = 91 W/m^2 via de atmosfeer (buiten het atmosferisch venster) de TOA, waar het vrij de ruimte in straalt. In werkelijkheid is dit getal hoger. Immers, bij de TOA is de gemiddelde uitstraling 239 W/m^2. Als je daar de 40 W/m^ (stralingsbalans Trenberth) van aftrekt, straalt de atmosfeer dus 199 W/m^2 uit.  Zoals ik al zei, de gebruikte getallen zijn fictief, en die 4 lagen zijn er in werkelijkheid schier oneindig veel. In ons model is te zien dat de emissie van langgolvige straling naar de ruimte dus op allerlei niveaus plaats vindt. Relatief weinig (maar met een hoge temperatuur) vanaf de lagen direct boven het aardoppervlak, en veel maar bij lagere temperaturen hoger in de troposfeer. Het “gemiddeld”  emissieniveau ligt op 5km hoogte, waar de temperatuur -18  °C is.

Volgens de Wet van Stefan-Boltzmann komt dat overeen met 239 W/m^2. Die Wet (of vergelijking) luidt  E = σT4 . In deze vergelijking is E de uitgestraalde energie, σ een constante (5.67 x 10^-8) en T is de temperatuur in Kelvin. Hier moet wel bij aangetekend worden dat het feitelijk onmogelijk is om het “gemiddeld emissieniveau ”  te bepalen. Je kunt dus stellen dat men, terug rekenend van 239 W/m^2 en gebruik makend van Stefan-Boltzmann, men uitkomt op -18 °C en de bij deze temperatuur horende  hoogte, 5 km,  het “gemiddeld emissieniveau” noemt. Doordat de temperatuur in de troposfeer afneemt met de hoogte zullen hogere (=koudere) lagen vanwege hun lagere temperatuur minder makkelijk energie uitstralen naar boven dan van onderen absorberen.

Wat gebeurt er nu als er bijvoorbeeld meer langgolvige straling absorberende stoffen in de atmosfeer komen, zoals bijvoorbeeld CO2 ? Dan neemt de transparantie af ( dus de opaciteit toe) , en dat geldt voor elke laag in het model.  Alleen het atmosferisch venter heeft nergens last van. Maar buiten het atmosferisch venster zal de uitstraling uiteindelijk minder worden. Stel dat de transparantie met 10% afneemt, dan daalt in bovenstaande model van 92 W/m^2 naar ongeveer 82 W/m^2.

Wat betekent dit nu voor de diverse lagen in de atmosfeer? Alle lagen worden door een toename van broeikasgassen minder transparant. Voor de lagen direct boven het aardoppervlak betekent dit dat de transparantie tot bijna 0 wordt teruggebracht. De lagen daarboven krijgen ook ‘last’  van verminderde transparantie. Alleen de TOA aan de bovenzijde kan nog steeds vrijelijk uitstralen. Uiteindelijk bereikt de langgolvige straling die vanaf het aardoppervlak uitgestraald wordt wel de TOA, maar er zijn onderweg meer broeikasgasmoleculen die de straling kunnen absorberen en naar alle kanten emitteren. Het gevolg hiervan is dat de onderste laag van de troposfeer nauwelijks nog in staat is om straling direct de ruimte in te zenden.

Hoe werkt dat?  Laten we nog eens terug gaan naar het model. In het model is de transparantie van de laag op 5 km hoogte (fictief) gesteld op 3%. Dat betekent dat slechts 3% van de langgolvige straling die deze laag naar boven emitteert, zonder onderweg geabsorbeerd te worden de TOA bereikt en uitstraalt naar de ruimte. Dus 97% van de straling uit die laag wordt op een of andere hoogte bovenin geabsorbeerd en geëmitteerd. Neemt nu de transparantie van de atmosfeer met 10% af als gevolg van een toename van broeikasgassen, dan kan nog slechts 2,7% ongehinderd de TOA bereiken.  De rest, 97,3% bereikt via de bovenliggende lagen (absorptie en emissie) de TOA. De laag op 5 km straalt dus minder langgolvige straling direct uit. Let op: dit is de laag met een relatief hoge temperatuur die relatief veel energie emitteert. De rest van de langgolvige straling uit die onderste laag wordt geabsorbeerd en geëmitteerd door hoger liggende lagen, die elk vanwege de toename van het broeikaseffect ook 10% minder direct naar de TOA kunnen uitstralen.  Alleen de allerhoogste laag, de TOA, heeft geen last van toegenomen broeikasgassen en emitteert alle resterende langgolvige straling de ruimte in.

Wat zijn de gevolgen? Dat de lagen onderin de troposfeer (de warmere lagen) minder uitstralen, en bijgevolg de hogere (koudere) relatief meer. Als je aan die langgolvige straling  meet die vanaf de TOA de ruimte ingaat, en je meet de zogenaamde “brightness temperature”, dan zul je dus een gemiddeld lagere temperatuur meten. Maar belangrijker is dat bij een lagere temperatuur een lagere energiestroom hoort. De energiestroom die de aarde verlaat wordt minder dan 239 W/m^2: de stralingsbalans is uit balans. En bij een lagere temperatuur hoort volgens Stefan-Boltzmann een energiestroom die dus ook kleiner is dan 239 W/m^2. Gevolg: het “gemiddeld emissieniveau”  schuift wat naar boven , naar een koudere laag.

Volgende keer meer.