Het tweede deel van de Britse serie “The Agenda” duikt in de klimaathysterie. Lighthouse.tv zorgde voor de Nederlandse ondertiteling. Must see.
Rode Kruis wenst u een fijne vakantie

Fig.1 Bron: Rode Kruis
Het Rode Kruis heeft al een aantal jaren een ‘klimaatbureau’. Waarom mag Joost weten, maar het Rode Kruis maakt klimaat spannend. Zoals recent met goede raad voor als je op vakantie gaat. Want op vakantie naar Zuid-Europa is gevaarlijk! Het Rode kruis adviseert om een vluchttas klaar te zetten:
“Zorg dat je belangrijke spullen snel kunt pakken als je plotseling moet vertrekken. Bij een natuurbrand of overstroming kan de stroom uitvallen, dus houd altijd een opgeladen powerbank bij de hand. Leg een kleine tas klaar met in ieder geval: paspoort, zorgpas of verzekeringsbewijs, powerbank, water en snacks, zaklamp en stevige schoenen. Zo kun je meteen weg als het nodig is.”
Ik heb mijn hele leven gekampeerd, en op de powerbank en snacks na heb je dan eigenlijk al automatische het hele lijstje bij je. Niet met de gedachte om te vluchten, maar om vakantie te vieren. Nu lijkt de oproep van het Rode Kruis meer op paniek zaaien dan op een serieuze raadgeving. De kans dat je in Zuid-Europa op de vlucht moet is erg klein. Hoe zit het bijvoorbeeld met die natuurbranden?

Fig.2 Bron: Bjorn Lomborg
Figuur 2 werd in 2023 door klimaateconoom Bjorn Lomborg gelanceerd. De onderliggende data zijn na te trekken door de links te volgen onder de grafieken. Minder natuurbranden, maar meer berichtgeving, dat is een bekend verschijnsel. Zo heeft de NOS in haar journaal ruim aandacht besteed aan het persbericht van het Rode Kruis, en veel kranten waren ook niet te beroerd om een berichtje over de materie te schrijven. Zo maak je mensen bang. Maar hoe zit het echt met die natuurbranden in Europa?
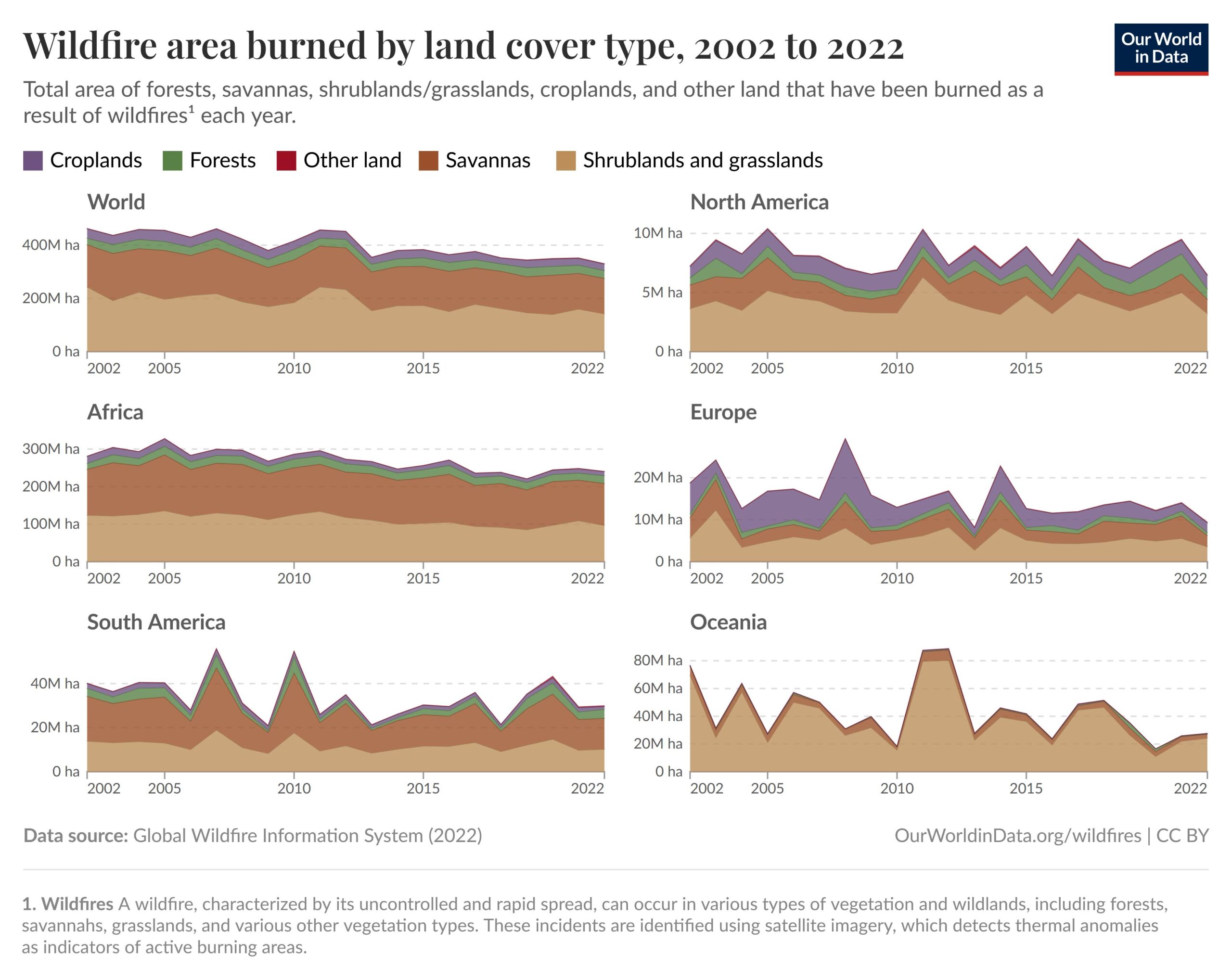
Fig.3 Bron: Our World in Data
De website Our World in Data levert grafieken op basis van data van 2002 t/m 2022. Figuur 3 toont het verloop van het oppervlak verbrande natuur voor de wereld als geheel en de 5 continenten. Pas op: de verticale schaal verschilt per grafiek! Wat meteen opvalt is dat het verbrande oppervlak in alle grafieken afneemt, behalve in Noord-Amerika.
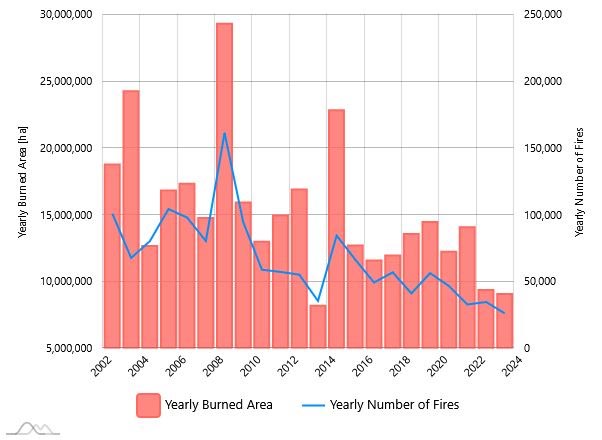
Fig.4 Bron: Global Wildfire Information System
Voor de Europese data keek ik naar de bron die Our World in Data gebruikt, namelijk het Global Wildfire Information System. De data lopen nu t/m 2023. In de grafieken van figuur 4 worden zowel de jaarlijkse verbrande oppervlak (staven) als het jaarlijks aantal branden (lijn) weergegeven. Beide grafieken tonen een duidelijk dalende trend: het verbrande oppervlak daalt van 2002-2023 met 50%, het aantal branden met maar liefst 66%.
Rode Kruis: “Ga je binnenkort op vakantie naar Zuid-Europa? Dan wil je natuurlijk ontspannen – niet hals over kop moeten vluchten voor bosbranden of noodweer. Toch gebeurt dat steeds vaker, ook op populaire plekken als Frankrijk, Griekenland en Italië.” Voor bosbranden is dat dus volstrekte onzin, integendeel zelfs: het aantal bosbranden is vanaf 2002 met 66% afgenomen.
Het zou het Rode Kruis sieren als ze zich vooral zouden bezig houden met hun primaire taak, het verlenen van noodhulp, en niet met klimaat. Klimaatactivisten zijn er al meer dan genoeg. Het NOS-journaal en de kranten zouden zich beter bezighouden met het verstrekken van echte informatie.
Flash flood in Texas
Fig.1 Bron: Mike Smith
Het waterpeil in de Guadalupe River in Kerr County, zuidelijk Texas, steeg op 4 juli 2025 met vele meters binnen 37 minuten. Dat gebeurde ‘s nachts, en gecombineerd met de snelheid waarmee het water kwam zorgde dat voor een catastrofale flash flood. Een flash flood is een plotselinge overstroming van laaggelegen gebieden. Flash floods komen vaak voor in droge gebieden waar plotseling veel neerslag valt.
Fig.2 Bron: Youtube
De video van figuur 2 laat niet alleen de snelheid zien waarmee de waterafvoer en waterhoogte toenamen, maar ook dat in korte tijd geen sprake meer was van een waterstroom maar van een kolkende massa van bomen, modder, stenen en huizen die van wege zijn snelheid en hoge dichtheid allesvernietigend was.
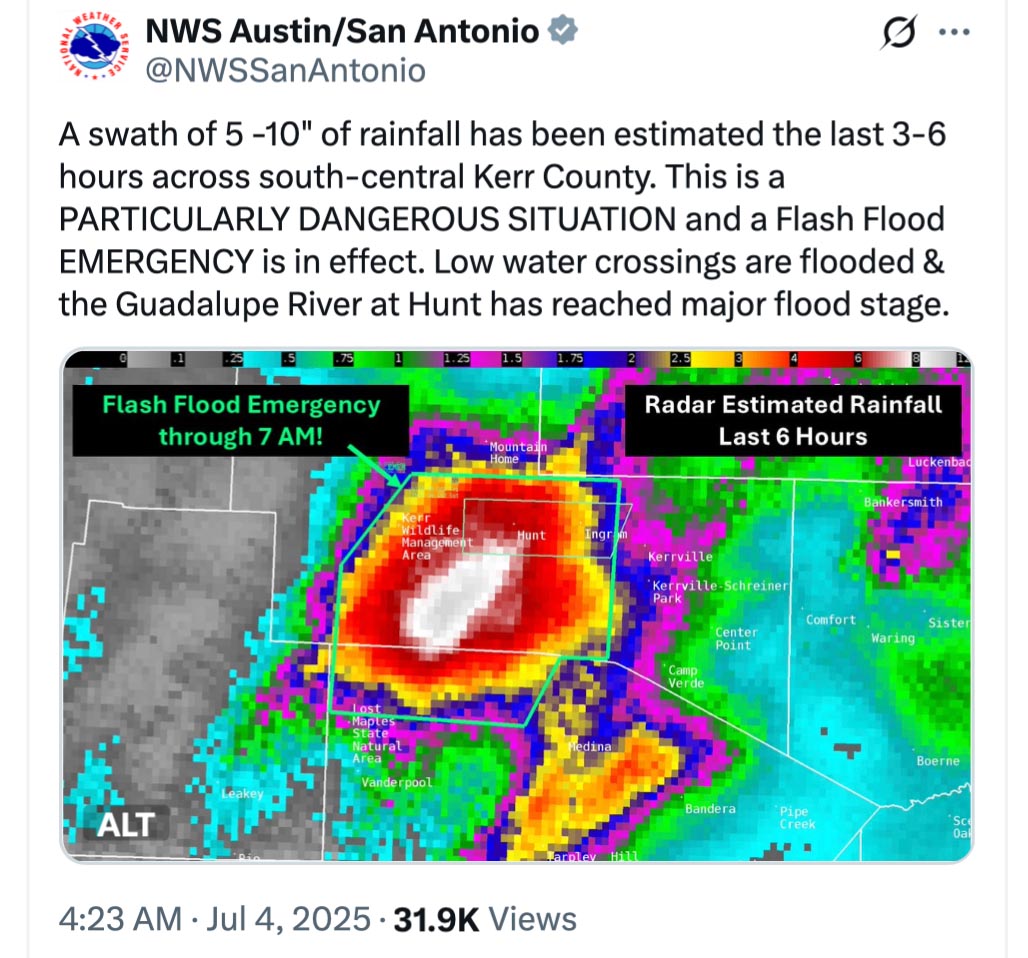
Fig.3 Bron: NWS
Er was in die nacht sprake van zeer intensieve neerslag in het gebied van Kerr County, met tot 10 inch (25 cm) regen in een tijdsbestek van 6 uur. Oorzaak was een samenspel van een restant van de Atlantische tropische storm Barry en van een tropisch systeem uit de Oost-Pacific. Dit systeem ontwikkelde zich tot onweersbuien die bleven hangen boven Centraal-Texas en zware regenval veroorzaakten, wat leidde tot dodelijke overstromingen. Een dergelijk weersysteem met grote hoeveelheden neerslag is in deze regio niet ongewoon, maar de intensiteit boven Kerr County was opvallend groot.
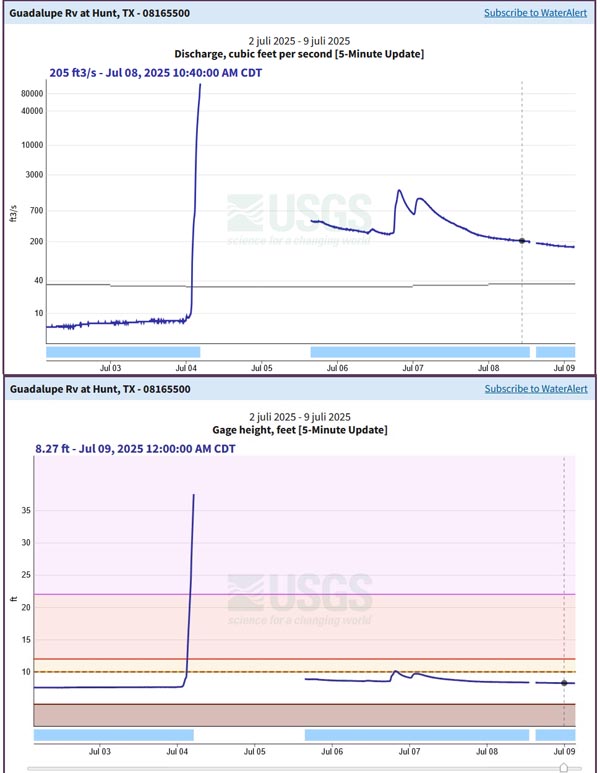
Fig.4 Bron: USGS
De grafieken in figuur 4 tonen de piekafvoer en waterhoogte in de Guadalupe River nabij Hunt (Kerr County). De waterhoogte gaat vanaf 02:00 uur op 4 juli stijgen (7.98 feet), en steeg in korte tijd op 05:10 uur al meer dan 12 meter. Toen oversteeg de data de capaciteit van de apparatuur, met als gevolg dat de data daarna ruim een etmaal ontbreken.
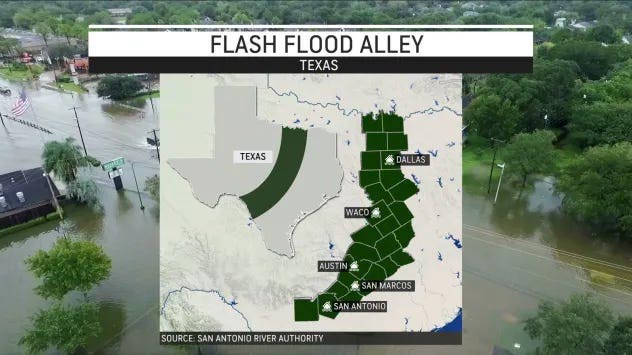 Fig.5 Bron: Accuweather
Fig.5 Bron: Accuweather
Dat Flash floods in dit deel van Texas niet ongewoon zijn bewijst de naam ‘Flash Flood Alley’ (figuur 5) voor het deel van Texas waar het verschijnsel regelmatig optreedt. Dat heeft natuurlijk deels te maken met het feit dat zware onweersbuien in het subtropische Texas niet ongewoon zijn. Maar ook buiten de Texaanse flash flood alley komen af en toe flash floods voor, zoals in het oostelijk deel van Kentucky en in West Virginia. Er moet dus meer aan de hand zijn dan het voorkomen van zware onweersbuien.
Niet alleen de intensiteit, de locatie en ruimtelijke spreiding van de neerslag spelen een grote rol, maar ook de aard van de ondergrond. Dan gaat het om bodemgebruik, topografie (relief), vegetatietypes en groei/dichtheid en bodemtype, die allemaal bepalen hoe snel een overstroming kan optreden.
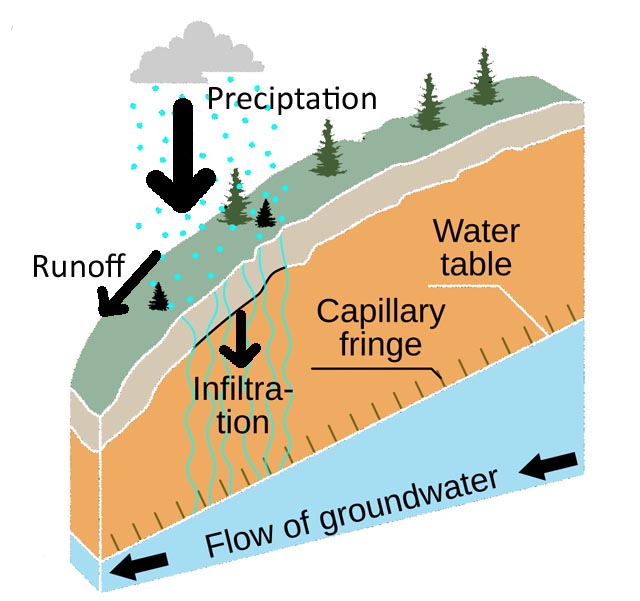
Fig.6 Naar: Wikipedia
Uiteindelijk gaat het hier om twee zaken: de neerslagintensiteit (liters/m2/uur) en de infiltratiecapaciteit van de bodem. Die laatste geeft de mate weer waarin de bodem in staat is neerslag op te nemen (en af te voeren naar het grondwater). Als die infiltratiecapaciteit kleiner is dan de neerslagintensiteit dan zal een deel van de neerslag bovengronds afstromen: run-off.
Zal de neerslag (grotendeels) door infiltratie naar het grondwater afgevoerd worden, dan zal die waterpiek sterk vertraagd en ‘uitgesmeerd’ in het dal terecht komen. Is de infiltratie gering, dan zal de neerslag grotendeels bovengronds (runoff) afgevoerd worden en een piekafvoer teweeg brengen in de rivier beneden in het dal. Dat laatste was in Texas het geval.
Fig.7 Bron: Youtube
Geoloog Philip Prince ging nader in op die overvloed aan runoff in Kenn County op 4 juli j.l., en ontdekte dat de geologie en geomorfologie van het landschap daarbij een grote rol speelden.
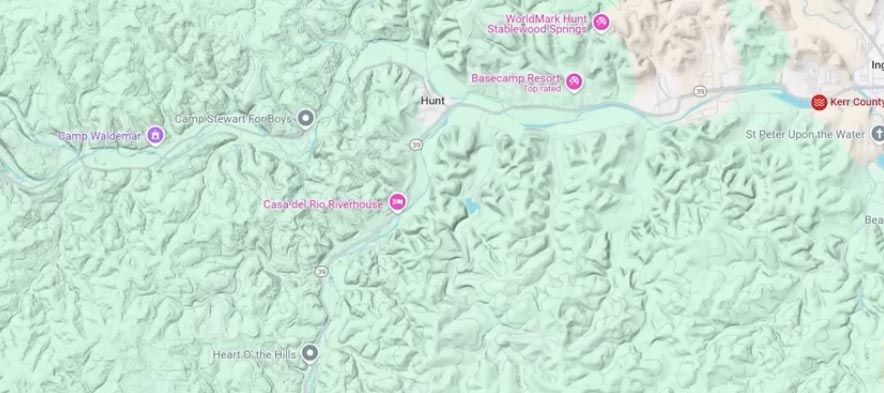
Fig.8 Bron: USGS
Figuur 8 laat zien dat hier sprake is van wat men in de USA een ‘high drainage channel landscape’. De rivier Guadalupe vertakt zich in schier oneindig veel zijtakken die het landschap doorsnijden. Dat wijst op een hoge runoff bij neerslag. Die zijtakken (die een groot deel van de tijd droog staan) strekken zich enkele honderden meters uit de heuvels in. Gevolg is dat er -op de vlakke dalbodem van de Guadalupe na- vrijwel overal hellingen zijn. Dat verhindert infiltratie. Bovendien stelt Prince dat het dagzomende gesteente (schalie) sterk horizontaal gelaagd is, wat runoff bevordert. En bij verwering ontstaan kleien die infiltratie verder verhinderen.
Philip Prince laat zien dat ook in andere streken die berucht zijn vanwege flash floods, zoals West Virginia en Eastern Kentucky, een vergelijkbaar reliëf en fijnmazige drainagestructuur aanwezig is. Bij zware neerslag ontstaan in combinatie met dat type landschap al snel flash floods.
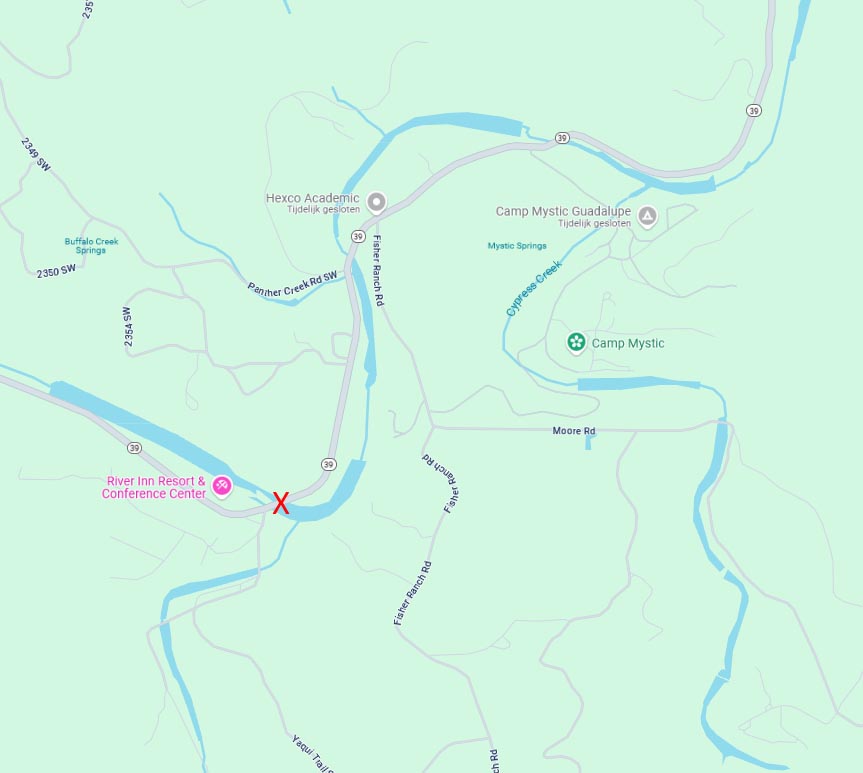
Fig.9 Bron: Google Maps
Figuur 9 laat de omgeving zien van de kampeerplaatsen langs de South Fork Guadalupe River. Goed is te zien dat de rivierafvoer gereguleerd is met een aantal (lage) dammen.

Fig.10 Bron: Google Maps
De foto van figuur 10 is genomen in april 2023, bij kalm weer. Het dal ligt er prachtig bij. De weg ligt op een dam (op figuur 9 aangegeven met een X), en verderop is de volgende dam al te zien. Dat flash floods hier geen zeldzaamheid zijn bewijst het feit dat elke dam een gele flood gauge heeft. Het gebeurt regelmatig dat de dammen onder water verdwijnen. De flood gauge toont dan of het verantwoord is om met de auto over te steken. Maximaal 5 feet is ongeveer 1.50 m. Bedenk dat de waterhoogte in de nacht van 4 juli 2025 steeg tot meer dan 12 m.!
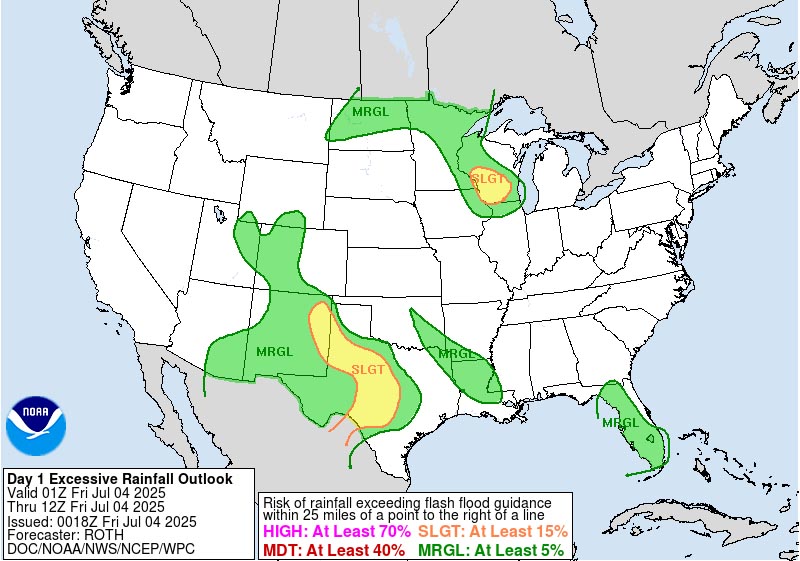
Fig.11 Bron: NOAA
Er is voor flash floods een waarschuwingssysteem in de USA. NCEP/NOAA levert dagelijks waarschuwingskaartjes, zoals die van figuur 11. Te zien is dat er een gevaarlijke situatie in delen van Texas aan het ontstaan is. De waarschuwing is voor de periode 01Z Fri Jul 04 2025 tot 12Z Fri Jul 04 2025. De tijdsaanduiding 01Z staat voor éé uur UTC (Coordinated Universal Time), ook wel bekend als Greenwich Mean Time (GMT). Omdat het in Texas 6 uur vroeger is dan in Greenwich geldt de waarschuwing voor 19u donderdag 3 juli tot 06 uur vrijdag 4 juli plaatselijke tijd. De waarschuwingskleuren geven geen extreme noodsituatie weer, maar gevaar voor een flash flood was er wel.
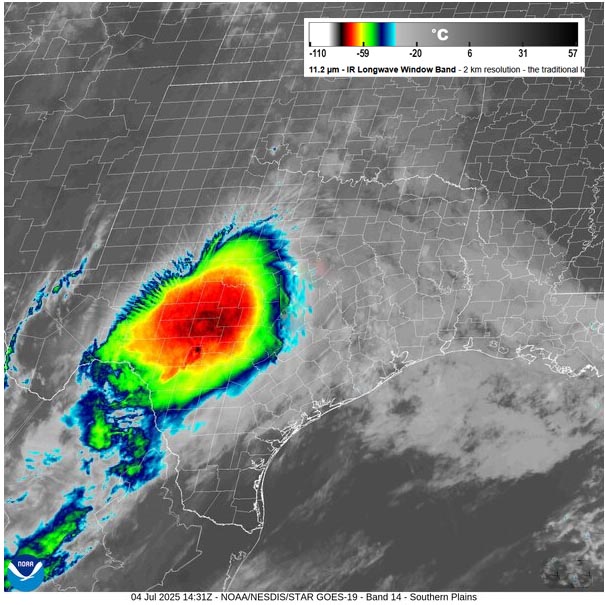
Fig.12 Bron: NOAA
Figuur 12 is een still uit de video op basis van satellietdata die de temperatuur van de bovenkant van wolken weergeven. De tijd is 14.31Z, dus 08 uur plaatselijke tijd. De top van de onweersbui is -80 a -90 graden C, wat wijst op een zeer hoge/zware onweersbui. Dat een dergelijke onweersbui lastig te voorspellen toont deze video van de ontwikkeling van onweersbuien boven Texas van 2 tot 7 juli 2025. Let op de snelheid waarmee een bui zich kan ontwikkelen en weer kan verdwijnen. Maar ook een poos kan blijven hangen waardoor enorme hoeveelheden neerslag naar beneden kunnen komen, zoals in de nacht van 4 juli 2025.
Hoe ongewoon is een dergelijke onweersbui zoals die op 4 juli in Kerr County viel? Probleem is dat we van de meeste locaties geen data hebben, en onweersbuien zijn zeer plaatselijk.
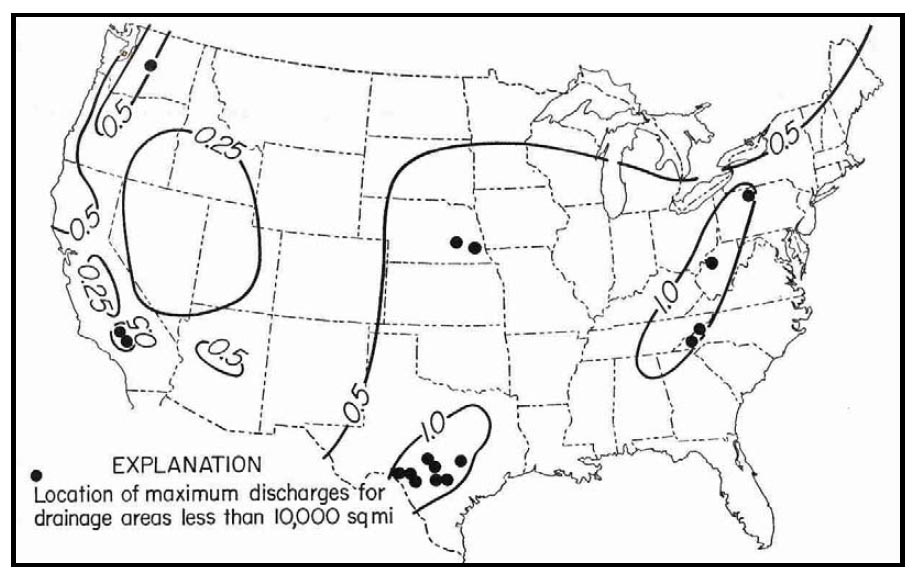
Fig.13 Bron: Hoyt + Langbein 1940
Figuur 13 laat zien dat dezelfde regio in Texas waar deze week overstromingen plaatsvonden al lange tijd (1940!) bekend staat als een brandhaard voor flash floods. Bijna een eeuw voor de publicatie van Hoyt en Langbein werd Texas zelfs geconfronteerd met een van de grootste verliezen aan mensenlevens in de Amerikaanse geschiedenis als gevolg van extreem weer. (bron: Roger Pielke Jr)
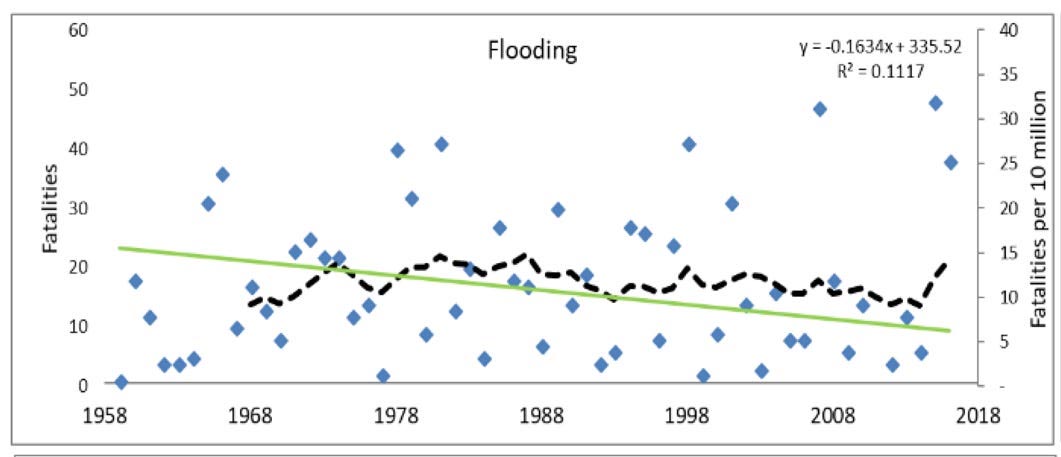
Fig.14 Bron: Roger Pielke Jr
Figuur 14 laat zien dat -terwijl de bevolking van Texas toenam van 9 miljoen in 1958 tot bijna 29 miljoen in 2018- het totale aantal doden door overstromingen door de tijd heen vrij constant bleef. Dat wijst er op dat allerlei maatregelen om slachtoffers van natuurrampen zoals flash floods te voorkomen, zeker helpen. Helaas zijn er bij de overstromingen van juli 2025 erg veel mensen omgekomen en nog velen vermist.
Er is echter globaal gezien een lichtpuntje: prof. Jonkman et al van TU Delft hebben recent een paper doen verschijnen getiteld “Floods have become less deadly: an analysis of global flood fatalities 1975–2022”.
De vissers hebben t gedaan
Soms, als ik een langere reis in de auto moet maken, probeer ik even naar NPO Radio1 te luisteren. Zo ook vorige week zaterdag rond 8:20u. Ik kreeg nog net een staartje mee van het NOS Radio1 Journaal. Een kort interview met de directeur van de Stichting De Noordzee, Ewout van Galen, naar aanleiding van een verdrag dat ondertekend zou moeten worden om ecosystemen in oceanen en zeeën te beschermen.
Nu ben ik wel gevoelig voor het beschermen van ecosystemen, maar met verstand, en op eerlijke wijze. Veel landen aarzelen om dat verdrag te ondertekenen, vaak omdat ze sterk afhankelijk zijn van de zee. Ook Nederland heeft (nog) niet getekend.
Eerst de gebruikelijke riedel over dat de oceanen zich in een ‘crisis’ bevinden, onder andere door ‘klimaatverandering’. Dat werd (uiteraard) door de mevrouw van het journaal zonder enige kritische wedervraag voor waar aangenomen.
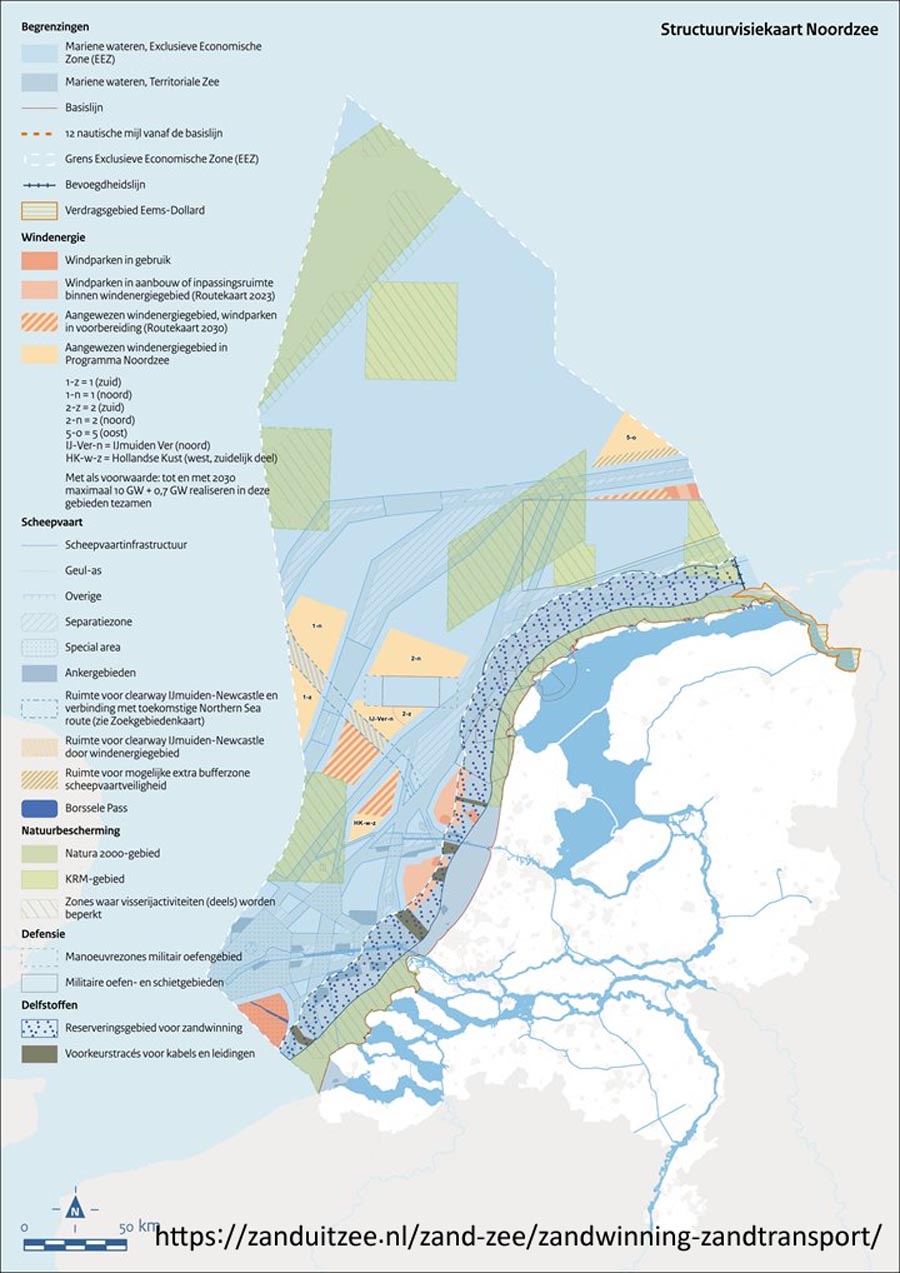
Nog bonter werd het toen de rol van ons land ter sprake kwam over het Nederlandse deel van de Noordzee. De bedreiging van het ecosysteem werd helemaal opgehangen aan de sleepnetvisserij. Nu mag dat best genoemd worden, maar tot mijn stomme verbazing kwamen andere verstorende activiteiten niet aan de orde, zoals windmolenparken, kabeltrajecten, baggerwerkzaamheden, gaswinning en ook grootschalige zandwinning. Wat dat laatste betreft: er is een gebied van 5134 km2 gereserveerd voor zandwinning, waar jaarlijks meer dan 20 miljoen m3 zand gewonnen wordt voor kustverdediging en andere zaken.
Kortom: ons deel van de Noordzee kent heel veel activiteiten die soms veel verstorender zijn voor water-ecosystemen dan de visserij. En dan is nog niet genoemd dat de Noordzee een van de drukst bevaren zeeën ter wereld is. Ik was dan ook hogelijk verbaasd dat het gesprek eigenlijk uitsluitend ging over bodemberoering door de Nederlandse sleepnetvisserij. Geen woord over windmolenparken of over de grootschalige delfstofwinning of over de andere activiteiten. Absurd!
Het verhaal van de directeur van Stichting De Noordzee was zeer eenzijdig en de mevrouw van het journaal deed haar plicht als journalist niet. Om te laten zien hoe druk het op de Noordzee is voeg ik een kaart toe uit de Structuurvisie 2022-2027. Een link naar het betreffende NOS journaal vindt u hier. Zeven minuten NOS Journaal was meer dan genoeg voor mijn geestelijke volksgezondheid. Pure propaganda.
Mijn hypothese duikt weer op
Gastbijdrage door Willis Eschenbach
Origineel in Engels: WUWT

Ik ben de afgelopen week op een bijzonder curieuze zoektocht geweest. Ik wilde al mijn WUWT-artikelen downloaden om ze om te zetten in e-books over verschillende onderwerpen. Om dat te doen, moest ik natuurlijk een aantal van mijn vroegste artikelen herzien. Bedenk wel: deze huidige analyse is het 1.051e artikel dat ik op WUWT heb geplaatst, dus het verbaast me niet dat ik me sommige helemaal niet meer herinner. Dat maakt het tot een interessante reis naar het verleden. Sommige artikelen bevatten theoretische veronderstellingen waarvoor ik destijds niet over de gegevens, computervaardigheden of gespecialiseerde functies beschikte die ik nu wel heb. Tegenwoordig kan ik een hele reeks data-analyses uitvoeren en visualiseren in de programmeertaal “R”.
Mijn eerste artikel voor WUWT was The Thermostat Hypothesis. Een versie daarvan werd later gepubliceerd als een wetenschappelijk artikel onder de naam The Thunderstorm Thermostat Hypothesis: How Clouds And Thunderstorms Control The Earth’s Temperature.
In dat artikel en in de publicatie legde ik mijn visie uit op hoe tropische onweersbuien en cumuluswolkenvelden functioneren als temperatuurregelaar van de tropen, en dus ook van de wereldtemperatuur. In de daaropvolgende jaren besefte ik dat dit mijn eerste teken was van wat ik later zag als een veel grotere verscheidenheid aan overlappende, individuele “emergente” klimaatverschijnselen die temperatuurvariaties tegenwerken.
Wat is een “emergent” verschijnsel eigenlijk? Laat ik mezelf citeren uit mijn artikel Emergent Climate Phenomena, dat ik je aanraad even te lezen. Een gemeenschappelijk kenmerk van emergente verschijnselen is dat het stroomsystemen zijn die ver van evenwicht opereren. Daardoor moeten ze zich voortdurend ontwikkelen en veranderen om te blijven bestaan. Ze zijn mobiel en veranderlijk, niet vast of onveranderlijk. En lokaal (dus uiteraard niet wereldwijd) kunnen ze entropie omkeren (de omgeving organiseren). Een andere naam voor emergente verschijnselen is dan ook “zelf-georganiseerde verschijnselen”.
Een ander kenmerk is dat ze spontaan ontstaan wanneer de omstandigheden goed zijn. Ze hoeven niet kunstmatig te worden opgewekt. Ze komen voort uit de achtergrond als reactie op lokale omstandigheden (temperatuur, vochtigheid, enz.) die een bepaalde drempel overschrijden.
Daarnaast hebben ze vaak een beperkte levensduur. Daarmee bedoel ik dat ze op een bepaald moment en op een bepaalde plaats ontstaan — meestal wanneer een lokale natuurlijke drempel wordt overschreden — waarna ze een bepaalde tijd blijven bestaan, en daarna verdwijnen. Wolken zijn daar een uitstekend voorbeeld van, net als onze eindige levensduur.
Emergente verschijnselen zijn ook meestal niet cyclisch, of hooguit pseudo-cyclisch. Ze herhalen zich niet op een regelmatige, geordende manier. Ze kunnen zich vaak vrij bewegen, en als dat zo is, is hun beweging moeilijk te voorspellen (zoals bij orkanen).
Een ander kenmerk is dat ze vaak gebaseerd zijn op temperatuur-drempelwaarden, meestal een lokaal temperatuurverschil. Ze verschijnen zelden onder die drempel, maar erboven kan hun aantal snel toenemen. Ook zijn ze vaak verbonden aan faseveranderingen in vloeistoffen — bijvoorbeeld wolken ontstaan door faseverandering van water.
Een laatste cruciaal kenmerk van drempel-gebaseerde emergente systemen: ze vertonen “overshoot” of hysteresis. In het geval van Rayleigh-Bénard-circulatie duurt het even voordat het systeem op gang komt bij een bepaalde temperatuurgradiënt. Maar als het eenmaal draait, blijft het functioneren, zelfs wanneer de temperatuur onder die drempel zakt. Deze hysteresis is nodig om systemen met vertraging succesvol te reguleren, systemen waarbij de reactie op veranderingen niet onmiddellijk is.
Samengevat: enkele kenmerken van emergente verschijnselen zijn:
- Stroomsystemen ver van evenwicht die spontaan ontstaan, vaak door een kritische (temperatuur)grens te overschrijden;
- Hun eigenschappen zijn niet voorspelbaar op basis van de onderdelen waaruit ze bestaan — niets in water- of luchtmoleculen voorspelt bliksem;
- Ze gedragen zich onvoorspelbaar;
- Vaak verbonden aan faseveranderingen;
- Ze vertonen vaak hysteresis (overshoot);
- Ze hebben een levensduur van begin tot einde;
- Hun patronen ontstaan uit vele kleine interacties.
Voor mij verklaart een en ander twee zaken. In de eerste plaats waarom moderne, geavanceerde weersmodellen maar een paar dagen vooruit betrouwbaar zijn — emergente verschijnselen zijn per definitie onvoorspelbaar. In de tweede plaats: moderne weer- en klimaatmodellen bevatten geen spontaan ontstane tropische onweersbuien. Het besef van spontane emergentie ontbreekt volledig.
Men probeert dus iets te analyseren dat niet bestaat — een wereld zonder emergente fenomenen — en doet dat met methodes die niet geschikt zijn voor de wereld die wél bestaat: een wereld die juist wordt gedomineerd door emergente fenomenen. Zie mijn artikel The Details Are In The Devil waarom dit simpelweg niet werkt.
Maar ik dwaal af. Tijdens het herlezen van die oude posts besefte ik dat ik nu beter in staat ben om de nauwkeurigheid van mijn eerdere beweringen over wolken en onweersbuien te testen. Mijn hypothese toen was dat wolken zowel opwaartse als neerwaartse temperatuurschommelingen tegengaan. Ik noemde ze een regulator (governor) in plaats van een eenvoudige feedback-reactie.
Klimaatwetenschappers spreken van “cloud feedback”. Maar wat wolken doen, is niet een ‘gewone’ lineaire feedback zoals die waar het IPCC over spreekt. Negatieve feedback zou alleen opwarming tegenwerken — hoe warmer, hoe sterker de tegenreactie.
Maar wolken zijn anders. Wolken en onweersbuien functioneren als een thermoregulerende regelaar. Ze vertragen niet alleen opwarming, ze verwarmen het oppervlak als het koud is en koelen het als het warm is. Vandaar dit artikel: ik bedacht een nieuwe manier om aan te tonen dat bovenstaande klopt. Uitleg:
De CERES-dataset bevat gegevens per graad (1° x 1°) over het “Surface Cloud Radiative Effect” (oppervlakte-wolkenstralingseffect), kortweg “CRE”. CRE is het verschil in stralingsenergie die het oppervlak bereikt mét of zonder wolken. Er zijn twee soorten: kortgolvig (zonlicht) en langgolvig (warmtestraling uit de atmosfeer). Samen vormen die het netto-effect van wolken, wat — afhankelijk van situatie en type wolk — zowel opwarming als afkoeling van het oppervlak kan betekenen.
Een negatieve CRE betekent dat wolken het oppervlak op die plek koelen, een positieve waarde betekent dat ze het verwarmen. Laat ik beginnen met een mondiaal overzicht van het CRE, om te laten zien waar wolken verwarmen of koelen en in welke mate.
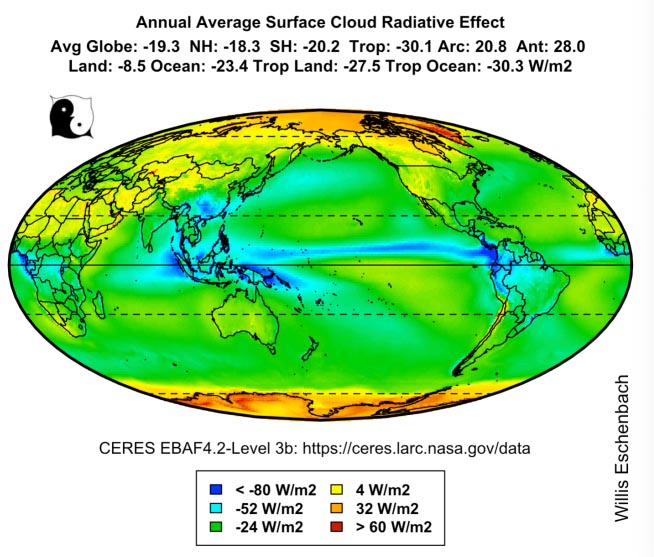
Fig. 1 Wereldwijde CRE (netto effect van kort- en langgolvige straling). Negatief = koelend, positief = verwarmend.
We zien een netto koelend effect van ongeveer -19 W/m². Maar dit laat niet zien hoe het effect verandert als de temperatuur op een locatie hoger of lager is dan het gemiddelde. Dat is wat het IPCC bedoelt met “cloud feedback”: ze beweren dat die positief is — dus dat wolken bij opwarming die opwarming versterken. Ik vond die claim altijd al zeer onwaarschijnlijk.
Voor mijn nieuwe aanpak keek ik naar het verschil tussen seizoensgebonden CRE (zomer en winter) en het jaarlijkse gemiddelde. Ik nam wereldkaarten van CRE in de zomer en winter, en trok daar telkens de kaart uit Figuur 1 van af. Daarna nam ik gemiddelde waarden per breedtegraad. Het resultaat:
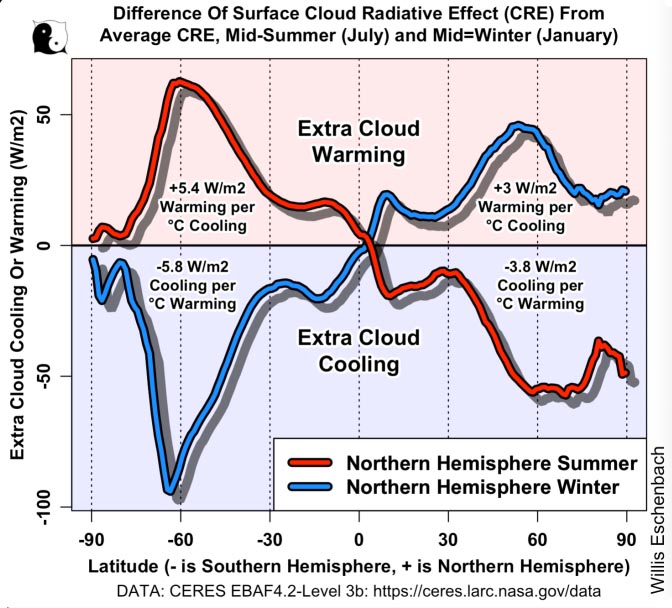
Fig. 2 Verschil per graad breedte tussen seizoens-CRE (zomer/winter) en jaarlijks gemiddelde.
Het resultaat verraste me. Het verschil is groot, regelmatig, en duidelijk. In het noordelijk halfrond tot 110 W/m² verschil, in het zuidelijk halfrond zelfs 160 W/m².
Bovendien: in de zomer koelen wolken het hele halfrond, van pool tot evenaar. In de winter doen wolken het tegenovergestelde: ze verwarmen het hele halfrond. Anders gezegd: als het warmer is dan normaal, koelen wolken het oppervlak; als het kouder is dan normaal, verwarmen ze het.
Aangemoedigd door deze bevinding, maakte ik kaarten van de wereld met die verschillen.
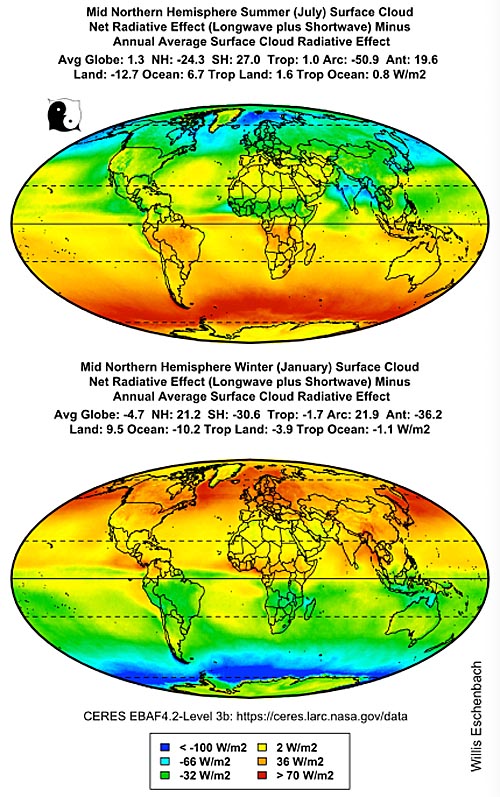
Fig. 3 Zomer- en winterverschillen in CRE ten opzichte van het jaar gemiddelde.
Dit geeft ons een andere blik op hoe het CRE verandert met de seizoenen. In de winter zorgen wolken voor extra opwarming, in de zomer voor extra afkoeling.
De wetenschappelijke toets van een hypothese is of ze leidt tot succesvolle, toetsbare voorspellingen. En de bovenstaande figuren bevestigen precies de voorspelling die ik vijftien jaar geleden deed: dat wolken en onweersbuien de aarde verwarmen wanneer het koud is, en koelen wanneer het warm is… wat valt daar níet aan te waarderen?
Eerste tropische dag

Fig.1 Bron: Telegraaf
Afgelopen vrijdag 13 juni 2025 werd op station De Bilt door het KNMI de eerste tropische dag gemeten met een maximum dagtemperatuur (Tx) van 31,8 °C. Een Tx van 30 °C of hoger wordt in Nederland een tropische dag genoemd. Nu werden op diezelfde dag in ons land op wel meer plaatsen temperaturen gemeten van 30 °C of hoger, maar die van De Bilt heeft een bijzondere status omdat alleen op dat station bepaald wordt of we te maken hebben met een hittegolf. Die 30,1 graden in het weerbericht (figuur 1), dat was om 12:30 uur. De Tx (maximum dagtemperatuur) liep in de loop van de middag op tot 31,8 °C.
Het weerbericht van de Telegraaf op 13 juni (gebaseerd op Weeronline) was wat langer dan ik in figuur 1 heb weergegeven, maar in die twee alinea’s staan voldoende opmerkelijke dingen om even bij stil te staan. Zo valt op dat gesproken wordt van de ‘klimaatperiode 1995-2024, wat ongewoon is. Het KNMI en vele andere organisaties hanteren voor een klimaatperiode als beginjaar altijd 1961, 1971 et cetera. Dus de meest recente klimaatperiode is 1991-2020.
Bovendien wordt er gesproken van een ‘gemiddelde eerste officiële tropische dag’ op 30 juni, wat me onzin lijkt. Beter lijkt me om te kijken hoeveel eerste tropische dagen in de periode van 1901 t/m 2024 er vroeger in het jaar vielen dan 13 juni en hoeveel later. Van de 99 eerste tropische dagen vielen er 29 vroeger dan 13 juni en 70 later dan 13 juni. Die 13 juni van 2025 is dus helemaal geen opzienbarend vroege datum voor een tropische dag. Verder vermeldt het weerbericht dat de ‘meest vroege’ (=vroegste) tropische dag op 9 mei 1976 gemeten werd. Ik kom uit op 1916, toen de eerste tropische dag in De Bilt gemeten werd op 5 mei. Hoe kan dat?
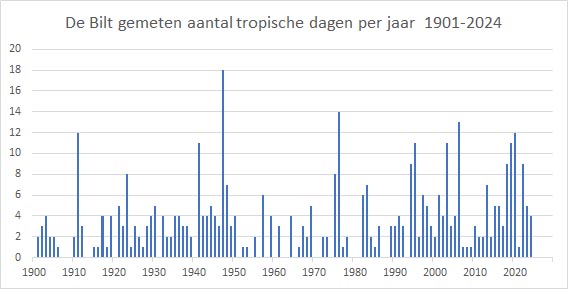
Fig.2 Data: KNMI
Figuur 2 toont het aantal op station De Bilt gemeten tropische dagen per jaar vanaf 1901 t/m 2024. Jaren met tropische dagen zijn – op de periode 1950-1990 na – redelijk gelijkmatig verdeeld in de tijd. Wel is er sprake van een toename van het aantal tropische dagen per jaar vanaf de jaren 1990. Het jaar 1947 steekt er echter met kop en schouders bovenuit met 18 tropische dagen, gevolgd door het jaar 1976 met 14 tropische dagen.

Fig.3 Data: KNMI daggegevens
Dat beeld wordt anders als we niet de gemeten data gebruiken, maar de in 2016 door het KNMI gecorrigeerde/gehomogeniseerde cijfers. Ik schrijf hier expres cijfers omdat er na homogenisatie geen sprake meer is van meetgegevens. Dat zijn de gehomogeniseerde data van 1901 tot 1 september 1951. Figuur 3 toont het resultaat van die homogenisatie voor het aantal tropische dagen per jaar.
Ik heb de periode waarin de data gehomogeniseerd zijn in de grafiek aangegeven. Door die homogenisatie werd het aantal tropisch dagen van 1901-1951 teruggebracht van 164 naar 60! Vergelijk de figuren 2 en 3 met elkaar. Verder zorgt die homogenisatie ervoor dat de toename van het aantal tropische dagen in figuur 3 veel groter lijkt dan in figuur 2.
Waarom heeft het KNMI die extreme correctie toegepast? Omdat er in 1950 en 1951 sprake was van een verplaatsing van de meetlocatie en wijziging van het instrumentarium. Dergelijke veranderingen hebben altijd invloed op de meetresultaten. De enige zuivere oplossing is in dergelijke gevallen dan om de oude tijdreeks af te sluiten en een nieuwe te starten. Maar instituten als het KNMI zijn dol op lange tijdreeksen en trachten daarom door homogenisatie (vaak ingewikkelde statistische bewerkingen) beide reeksen aan elkaar te ‘plakken’.
Fig.4
Over die opmerkelijke homogenisatie van De Bilt is tweemaal wat geschreven. In 2019 verscheen het bovenstaande rapport dat uitgebreid de homogenisatie uit 2016 beschrijft. Dat Nederlandstalige rapport is hier downloadbaar. Dat rapport werd in 2021 gevolgd door een peer reviewde publicatie getiteld “Reassessment of the homogenization of daily maximum temperatures in the Netherlands since 1901”. Beide publicaties tonen aan dat de homogenisatie van de temperaturen in De Bilt niet deugt.
Helaas is het zo dat tegenwoordig op de webpagina van de KNMI daggegevens alleen de gehomogeniseerde cijfers beschikbaar zijn. Het zou fair zijn als het KNMI ook de ‘niet gecorrigeerde’ temperatuurdata van station De Bilt zou tonen, in elk geval totdat die homogenisatie uit 2016 gecorrigeerd is.
Dr. Ferdinand Meeuws geïnterviewd
Ferdinand Meeus is een Belgische chemicus met een doctoraat in de chemie, fotofysica en fotochemie van de KU Leuven. Na zijn pensionering heeft hij zich toegelegd op klimaatvraagstukken en profileert hij zich als ‘klimaatrealist’.
Onlangs werd hij geïnterviewd door een journalist van Indepen Nieuws. Half uurtje luisteren, aanrader!
Boven/onder de ‘normale’ temperatuur
Vaak hoor of lees je bij het weerbericht dat de temperatuur die dag lager of hoger is dan normaal voor de tijd van het jaar. Maar wat is normaal?
Het leuke is dat in de weerkunde het begrip ‘normaal’ officieel gebruikt wordt. Het KNMI stelt om de tien jaar het gemiddelde weer in ons land vast. In de meteorologie wordt dit ‘de normaal’ genoemd. Die normaal wordt berekend voor een aantal meteorologische grootheden zoals temperatuur en neerslag over een periode van dertig jaar. De laatste keer ging dat om de periode 1991-2020. Eerdere tijdvakken zijn 1981-2010, 1971-2000 enzovoort. Gebruikelijk is dat men bij vergelijkingen het laatste tijdvak gebruikt, maar er kunnen redenen zijn om daarvan af te wijken.
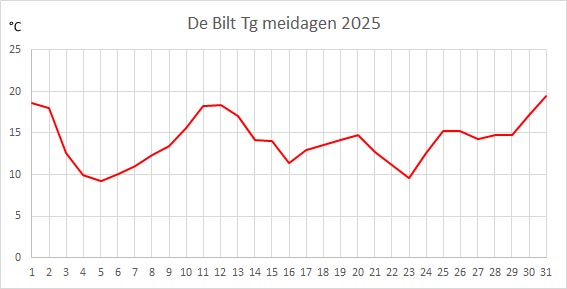
Fig.1 Data: KNMI
In de grafiek van figuur 1 ziet u het verloop van de gemiddelde etmaaltemperatuur voor de meidagen van 2025. De lijn is nogal springerig, volatiel, maar dat hoort bij het Nederlandse weer. Zou het elke dag windstil en wolkeloos zijn geweest dan zou de lijn tamelijk recht en licht oplopend zijn geweest. Maar omdat de bewolking van dag tot dag verschilt en het meestal waait bepalen die factoren de temperatuur in ons land. Omdat Nederland op gematigde breedte op de grens van oceaan en continent ligt maakt het nogal wat uit waar de lucht vandaan komt (brongebied). Vandaar dat springerige karakter.
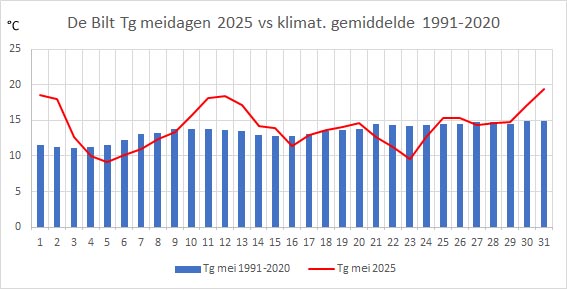
Fig.2 Data: KNMI
In figuur 2 zijn met blauwe kolommen de ‘normale’ temperaturen per meidag toegevoegd. Dat is op basis van het meest recente tijdvak 1991-2020. Te zien is dat door het middelen van steeds 31 dagen het springerige uit die kolommen grotendeels verdwenen is. Dat middelen levert dus een ‘gesmoothed’ verloop op. Het gevolg is dat de springerige dagtemperatuur van mei 2025 daardoor de ene keer boven en de andere keer onder de ‘normale’ temperatuur ligt. Dat ligt niet aan mei 2025 want die maand heb ik zonder bijbedoelingen gebruikt. Dat geldt voor elke willekeurige maand.
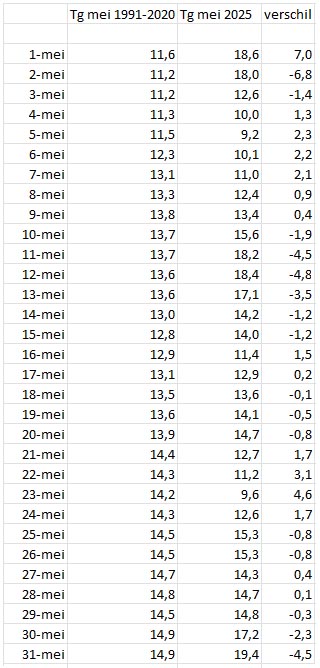
Fig.3 Data: KNMI
De tabel in figuur 3 laat zien dat er in feite geen enkele dag in mei 2025 was waarvan de temperatuur gelijk was aan de ‘normaal’. Van de 31 meidagen van 2025 lag de gemiddelde etmaaltemperatuur 17 maal boven en 14 maal onder de normaal. In feite zou je kunnen stellen dat het zinloos is dat weermannen/-vrouwen regelmatig vermelden dat de temperatuur die dag lager of hoger is dan normaal. Dat is namelijk vrijwel altijd het geval. En ‘warmer dan normaal’ wél vermelden maar ‘kouder dan normaal’ niet is uiteraard uit den boze. Andersom natuurlijk ook .
Droge dagen
Droogte is tegenwoordig ‘hot’. Dat heeft wellicht te maken met het feit dat droogte door sommigen graag geassocieerd wordt met menselijke invloed op het klimaat. Het KNMI gebruikt van april tot oktober de Droogtemonitor.
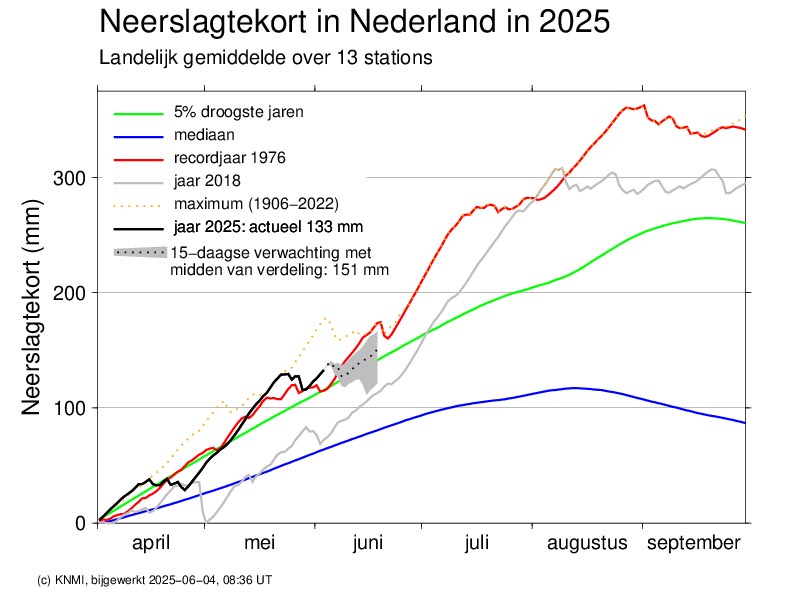
Fig.1 Bron: KNMI
Het neerslagtekort volgens het KNMI is het verschil tussen neerslag en potentiële verdamping van april tot oktober. Beter zou zijn van april t/m augustus, want in die periode is de verdamping in ons land groter dan de neerslag, zie figuur 2:
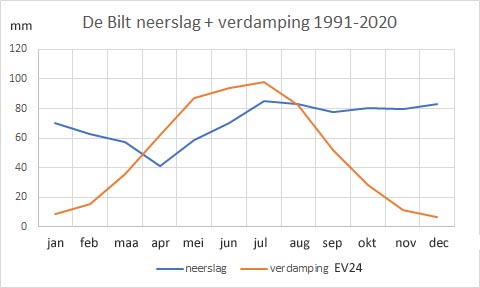
Fig.2 Data: KNMI
Nu moet men dat begrip ‘neerslagtekort’ niet al te letterlijk nemen, want of er sprake is van een echt ‘tekort’ (=probleem, dus aanvulling gewenst) is sterk afhankelijk van de plaatselijke omstandigheden. Neerslag en verdamping zijn meteorologische data, die zeggen niet alles over de vraag of bijvoorbeeld boeren of natuurgebieden last hebben van droogte. Factoren die daarbij meespelen zijn de hoogteligging, grondsoort, bodemtype, bodemgebruik en nog wat andere dingen. Daarover later meer.
In dit inleidend artikeltje kijk ik alleen maar naar de neerslag en het aantal droge dagen. Dat doe ik voor station De Bilt, waarvan de geografische ligging een aardig gemiddelde voor het land is.
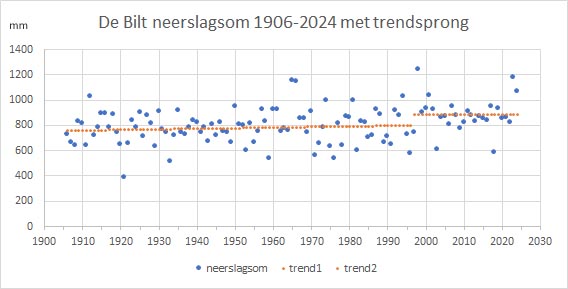
Fig.3 Data: KNMI
Vanaf 1 januari 1906 zijn de daggegevens van de neerslag op station De Bilt voorhanden. Op basis daarvan heb ik de jaarsommen berekend en weergegeven met blauwe puntjes. Over de hele periode 1906-2024 is er sprake van een stijgende trend, van 734 mm/jaar naar 873 mm/jaar.
Wat opvalt is dat die stijging niet geleidelijk verloopt maar dat er rond 1996 sprake is van een sprong van ~100 mm. Van 1906 t/m 1996 is er sprake van een trend van 4,5 mm/decennium, die vanaf 1997 halveert tot een trend van 2,2 mm/decennium.
Het KNMI verwijst voor wat betreft de toename van de neerslag naar de Clausius-Claperonvergelijking. Die geeft een verband tussen de temperatuur van lucht en de hoeveelheid water die lucht kan opnemen. Bijvoorbeeld: bij een temperatuurstijging van 1 graad kan de hoeveelheid water toenemen met 7 procent. Dus: hogere temperaturen kunnen leiden tot meer neerslag, maar dat is geen wet van Meden en Perzen. Kijk maar naar de volgende grafiek:
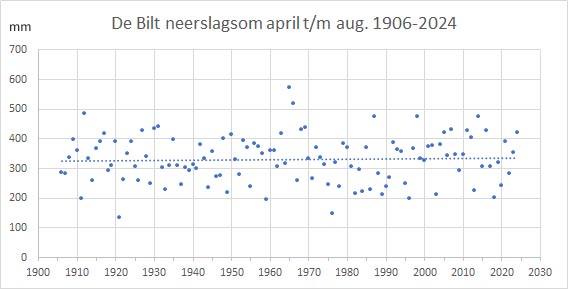
Fig.4 Data: KNMI
In figuur 4 heb ik gekeken naar de jaarlijkse neerslagsommen voor de maanden april t/m augustus, de lente- en zomermaanden waarin in Nederland de verdamping groter is dan de neerslag. Als je deze grafiek vergelijkt met die van figuur 3 dan valt op dat de trendbreuk verdwenen is. Bovendien is voor de hele periode 1906-2024 nauwelijks sprake van een trend. Dat is bijzonder, omdat figuur 4 de warmste maanden van het jaar betreft. Blijkbaar houdt de werkelijkheid zich van april-augustus niet zo goed aan de Clausius-Claperonvergelijking.
Uit genoemde daggegevens van station De Bilt voor de maanden april t/m augustus haalde ik het aantal droge dagen (neerslag = 0 mm):
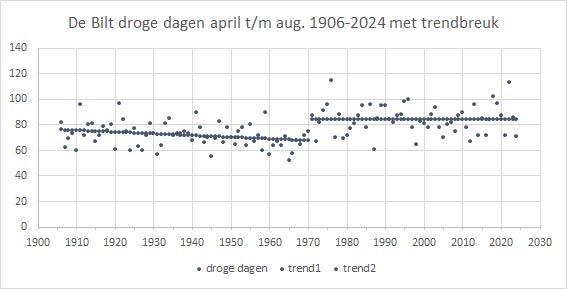
Fig.5 Data: KNMI
Anders dan bij de grafiek van figuur 4 is hier sprake van een sprong in de data rond 1970. Vóór de sprong is het aantal droge dagen lager en de trend licht dalend, ná de sprong is het aantal droge dagen hoger en een trend afwezig. De sprong is dermate opvallend dat ik in eerste instantie dacht aan verandering in metadata (meetlocatie, instrumentarium). De KNMI metadata voor neerslagmeting lieten echter geen veranderingen rond 1970 zien voor het station De Bilt:

Fig.6 Bron: KNMI
Ik vermoed daarom dat de sprong veroorzaakt is door een ‘permanente’ verandering in de luchtcirculatie boven Nederland.
Nu hebben droge dagen meer effect als ze ‘gebundeld’ voorkomen, dat wil zeggen dat een langdurige droge periode meer bijdraagt tot een droogte-effect dan een of enkele droge dagen, afgewisseld met regenachtige dagen. Daarom heb ik ook gekeken naar de lengte van de droge periodes van april-augustus, met als ondergrens ≥14 droge dagen:
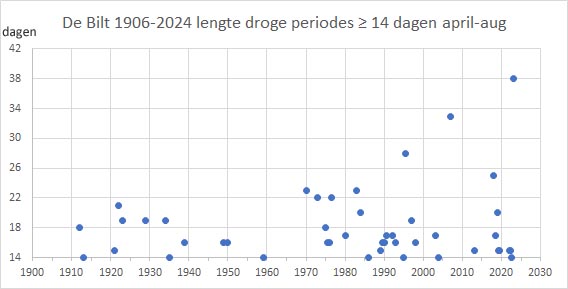
Fig.7 Data: KNMI
De grafiek van figuur 7 laat zien dat er inderdaad sprake is van relatief méér langdurige droogteperiodes vanaf 1970. Bovendien is er na 1970 sprake van langduriger droge periodes dan voordien. Na 1970 komen er maar liefst 8 droge periodes voor van meer dan 3 weken tot meer dan een maand, terwijl die in de periode vóór 1970 ontbreken.
Ik vermoed dat de sprong in de grafiek van het aantal droge dagen (figuur 5) en de sprong in de data van de lengte van de droge periodes (figuur7) veroorzaakt is door een ‘permanente’ verandering in de luchtcirculatie boven Nederland rond 1970. Onderzoek daarnaar heeft vaker plaatsgevonden, onder andere door het KNMI, en door mijzelf. Maar de gevolgde methode op basis van de windrichting kent zo zijn beperkingen.
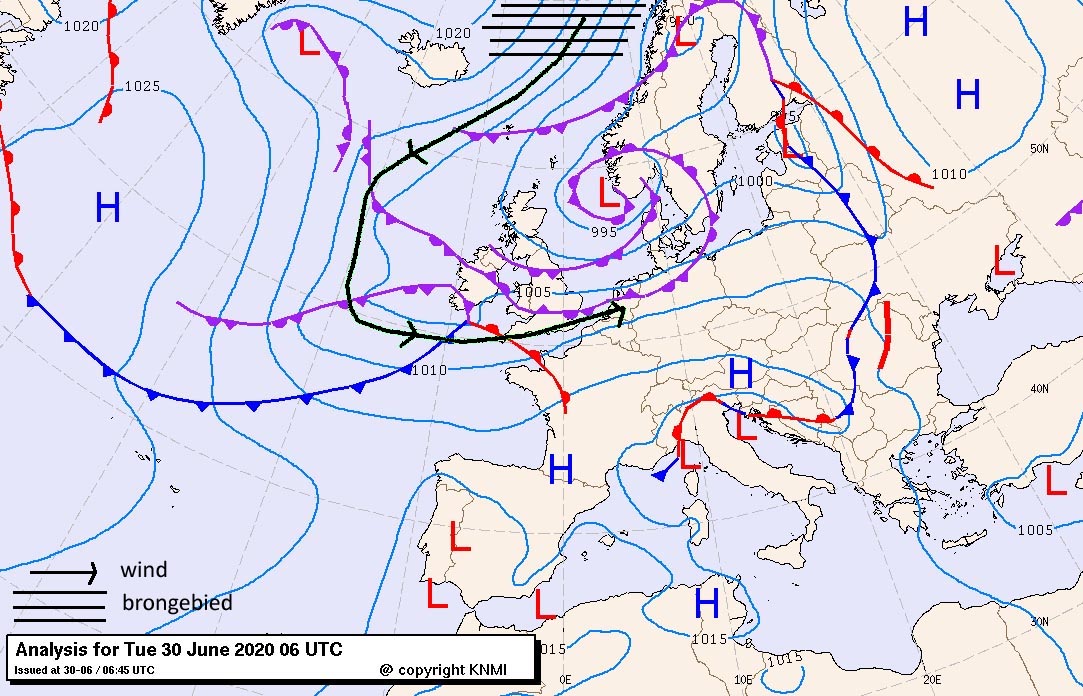
Fig.8 Bron: KNMI weerkaart
De windrichting is de hoek waaruit de wind in De Bilt waait. Maar de wind komt vaak met een grote bocht naar Nederland, afhankelijk van de ligging van hoge- en lagedrukgebieden. Figuur 8 laat als voorbeeld de situatie op 30 juni 2020 zien. In De Bilt meten we dan ZW wind, maar die lucht komt helemaal niet uit het ZW, maar met een grote bocht vanaf het noordelijk deel van de Atlantische Oceaan vandaan (zwarte pijl). Het brongebied ligt tussen Groenland en Noorwegen. Dit subarctische brongebied (horizontale zwarte streepjes) bepaalt sterk de eigenschappen van de lucht die dan bij ons binnen waait. Niet de windrichting gemeten in De Bilt maar de eigenschappen van het brongebied en van het traject richting Nederland bepalen uiteindelijk de weerkenmerken in Nederland op die 30 juni 2020.
Beter zou dus zijn om niet te kijken of er met de windrichting in Nederland wat gebeurt rond 1970, maar of er veranderingen plaatsvinden in het brongebied van de binnenkomende luchtmassa’s. De Duitse weerdienst heeft het dan over Grosswetterlagen (GWL). Gelukkig zijn die veranderingen in brongebied van de luchtmassa’s die het weer in Nederlad bepalen een paar jaar geleden door Jippe Hoogeveen voor alle dagen vanaf 1838 in kaart gebracht. Dat werk mondde uit in een prachtige publicatie van zoon en vader Hoogeveen.
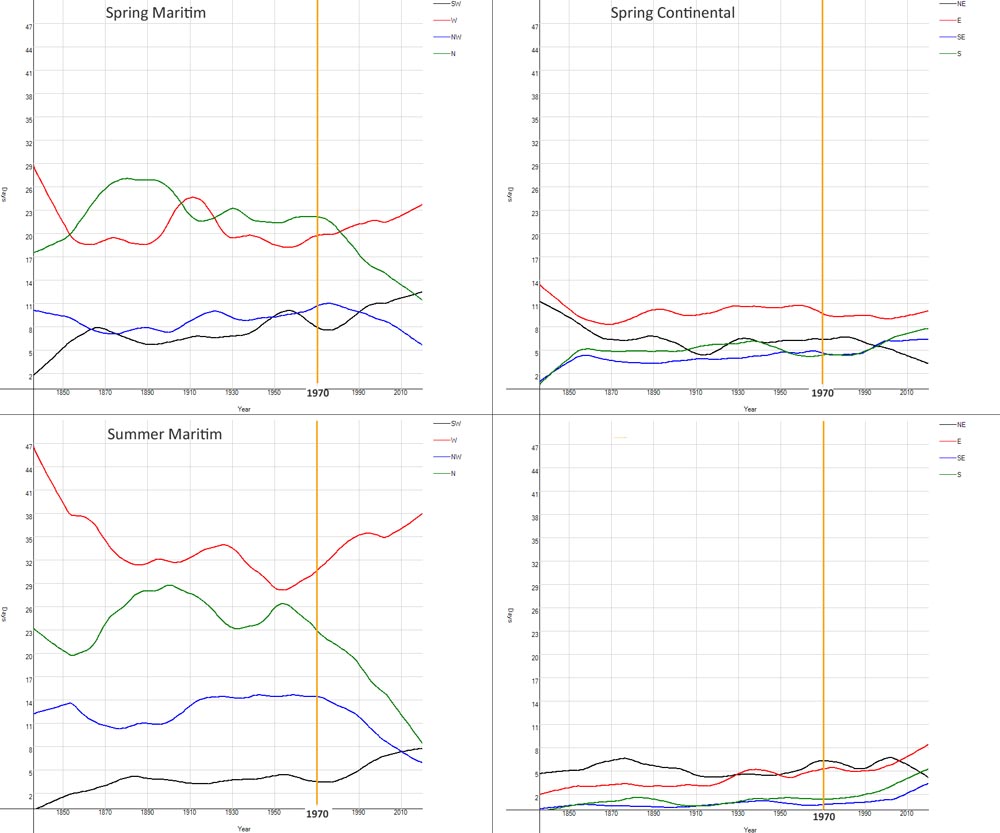
Fig.9 Naar: Hoogeveen en Hoogeveen
In figuur 9 heb ik een viertal grafieken uit die publicatie van Hoogeveen en Hoogeveen samengebracht, die de veranderingen in luchtcirculatie van 1836 tot 2020 tonen. SW, W, NW en N hebben betrekking op de ligging van de brongebieden ten opzichte van Nederland. Maritim betekent brongebied boven zee, Continental brongebied boven land.
Omdat dit artikel gaat over de droogte heb ik alleen gekeken naar de grafieken van lente en zomer. Direct is te zien dat rond 1970 er in de luchtcirculatie sterke veranderingen plaatsvinden. Het is niet moeilijk om die veranderingen te vertalen in ‘meer warmte’. Immers, zowel voor maritieme als continentale luchtsoorten is er sprake van een sterke verschuiving van meer noordelijke naar meer zuidelijk gelegen brongebieden.
Lastiger is het om die veranderingen één op één te vertalen in ‘toenemende droogte’, maar dat die veranderingen in luchtcirculatie groot effect hebben gehad op het weer in Nederland hebben vader en zoon Hoogeveen klip en klaar aangetoond.
Dat die weersveranderingen ook hebben gezorgd voor een sterke toename van de hoeveelheid zonlicht (door afname van bewolking) heb ik al een paar keer laten zien. Niet alleen in Nederland maar ook in grote delen van West Europa. Meer zon en minder bewolking betekenen meer kans op droogte.
Fig.10 Bron: ECMWF
Op weg naar blackout stroomnet?
Zonder energie staat alles stil. In de huidige tijd van energietransitie richting 0% fossiel is het daarom van immens belang om de haalbaarheid van die energietransitie in de gaten te houden. Lopen we tegen de grenzen van wat mogelijk is aan? Daar lijkt het wel op.
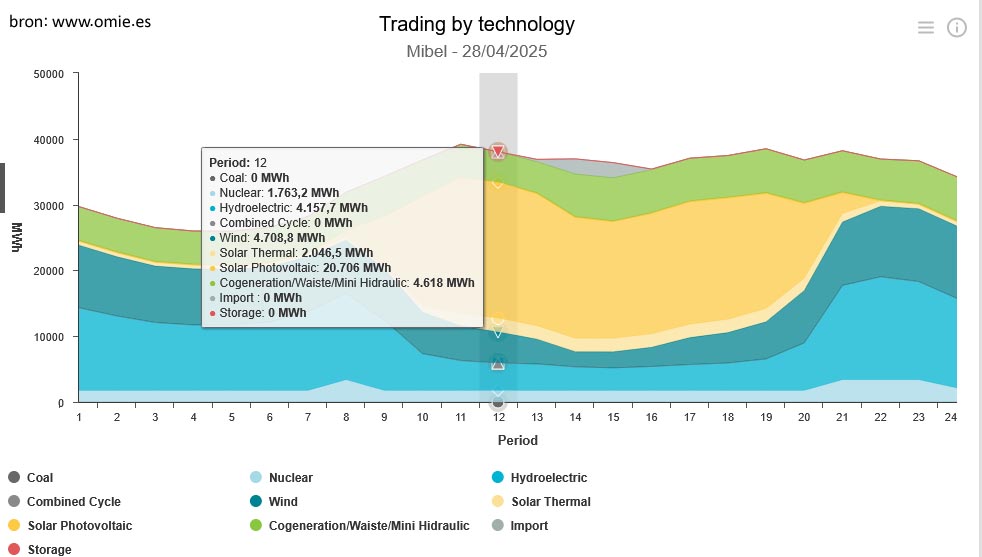
Fig.1 Bron: OMIE
Op 28 april 2025 viel in vrijwel geheel Spanje en Portugal voor vele uren de stroom uit. Wat gebeurde daar? De autoriteiten zijn op dit moment nog steeds op zoek naar de oorzaak van de uitval. Maar gelukkig hebben zich al diverse deskundigen over de kwestie uitgesproken, zoals Raúl Bajo Buenestado van het Rice University’s Baker Institute for Public Policy in Houston, Texas.
Hij beschrijft in zijn analyse de toedracht:
“ Rond 12:30 uur lokale tijd in Spanje — enkele minuten vóór de instorting van het netwerk — werd 78% van de elektriciteit in het Iberisch systeem opgewekt uit hernieuwbare bronnen, waarvan bijna 60% afkomstig was van zonne-energie. Ter vergelijking: conventionele technologieën, zoals gas- en kerncentrales, leverden slechts zo’n 15% van de totale opwekking. Deze verdeling is niet ongebruikelijk in Spanje of Portugal, waar een hoog aandeel hernieuwbare opwekking normaal is op zonnige en winderige dagen.
Wat 28 april echter uitzonderlijk maakt, is dat volgens de Spaanse netbeheerder Red Eléctrica de España twee opeenvolgende verliezen (uitval) in de opwekking plaatsvonden in het zuidwesten van Spanje, vermoedelijk door grote zonne-installaties. De exacte oorzaken worden nog onderzocht. Door de beperkte beschikbaarheid van conventionele opwekking en verminderde ondersteuning vanuit buurlanden — mede door het loskoppelen van het Franse netwerk — ontstond een “perfecte storm” die leidde tot een massale stroomuitval.
Binnen vijf seconden verloor Spanje ongeveer 15 gigawatt aan capaciteit, gelijk aan 60% van de nationale elektriciteitsvraag. De resterende opwekking was onvoldoende om in de vraag te voorzien, wat leidde tot een kettingreactie van uitval door het hele netwerk. Diverse productie-eenheden werden automatisch losgekoppeld ter bescherming van de infrastructuur, en kerncentrales werden conform veiligheidsprotocollen stilgelegd.
Binnen enkele uren was het volledige Iberisch Schiereiland zonder stroom. Het hele vasteland van Spanje en Portugal zat tegelijk zonder elektriciteit, een situatie die urenlang aanhield.
Er was een black start nodig — een proces waarbij het systeem van nul wordt herstart. Aanvankelijk gebeurde dit met interne opwekking. Later speelden ook de beperkte interconnecties met buurlanden een sleutelrol: Marokko leverde tot 900 megawatt via lijnen over de Straat van Gibraltar, en Frankrijk droeg tot 2 gigawatt bij. Het herstel verliep geleidelijk en ongelijk over de regio’s.
Diezelfde dag kwam de stroom rond 17:00 uur lokaal weer op gang en herstelde zich verder in de loop van de avond en nacht. Tegen 6:00 uur op 29 april was 99% van de nationale vraag hersteld, wat beschouwd wordt als een relatief snelle en succesvolle black start. Tegen die tijd had het incident echter al geleid tot meerdere slachtoffers, waaronder duizenden mensen die vastzaten in treinen, liften en andere systemen die afhankelijk zijn van elektriciteit.
Het risico op grootschalige black-outs in elektriciteitssystemen met een hoog aandeel hernieuwbare energie is al langer bekend. De black-out van 28 april maakt deze kwetsbaarheden echter pijnlijk zichtbaar. ”

Fig.2 Bron: Klimaatgek
Het zwakke punt bij stroomopwekking door wind en zon zijn frequentieregeling en inertie. Die worden traditioneel geleverd worden door synchrone generatoren in conventionele centrales, zoals kern-, thermische en waterkrachtcentrales. Deze leveren elektrische inertie via roterende massa’s, wat helpt om de netfrequentie en spanning stabiel te houden bij plotselinge fluctuaties of onbalans. Vergelijk het met het vliegwiel van een automotor.
Zonne- installaties werken echter met ‘grid-following’ omvormers — apparaten die afstemmen op een bestaande netfrequentie en spanning- in plaats van die zelf op te wekken. Een dergelijk apparaat gebruiken alle eigenaren van zonnepanelen om hun panelen aan te sluiten op het stroomnet. De omvormer meet de netspanning en netfrequentie en past zijn output daaraan aan. Deze systemen zijn afhankelijk van een stabiel net en kunnen dus niet autonoom bijdragen aan netstabiliteit bij verstoringen.
Naarmate het aandeel op omvormers gebaseerde opwekking toeneemt en conventionele (gas, kernenergie, steenkool) opwekking afneemt, wordt het net kwetsbaarder voor verstoringen — zoals op 28 april op het Iberisch Schiereiland het geval was. De opwekking op dat moment was voornamelijk zonne-energie (~60%), wind (~12%), met weinig conventionele ondersteuning. Die conventionele ondersteuning met gas is in figuur 1 te vinden onder ‘cogeneration’ (~12%), terwijl kernenergie nog geen 5% leverde. Die situatie betekende dat het systeem de schokken van de verliesincidenten niet kon opvangen. Automatische beschermingsmechanismen werden geactiveerd, wat leidde tot een kettingreactie van uitval.
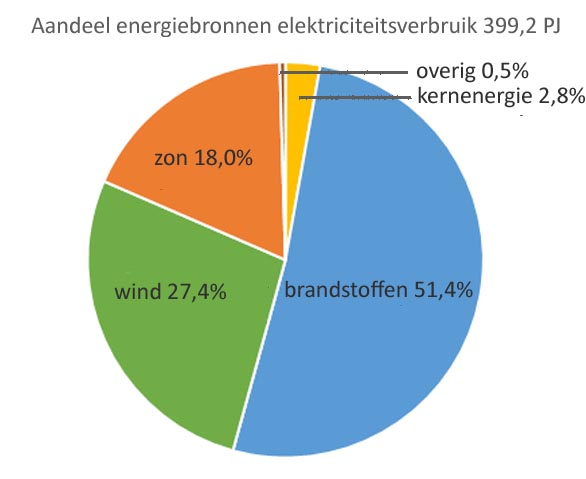
Fig.3 Data: CBS
De grafiek van figuur 3 toont het aandeel van de diverse energiebronnen in het elektriciteitsverbruik in Nederland gemiddeld over het jaar 2024. Zon en wind namen 45,4% van de totale productie voor hun rekening, waarvan zonne-energie ‘slechts’ 18%. Maar bedenk dat dit een jaargemiddelde is, op een zonnige zomers dag kan de opwekking van elektriciteit door zon en wind groter worden dan de vraag naar elektriciteit. Wat dat voor gevolgen kan hebben ziet u hier:
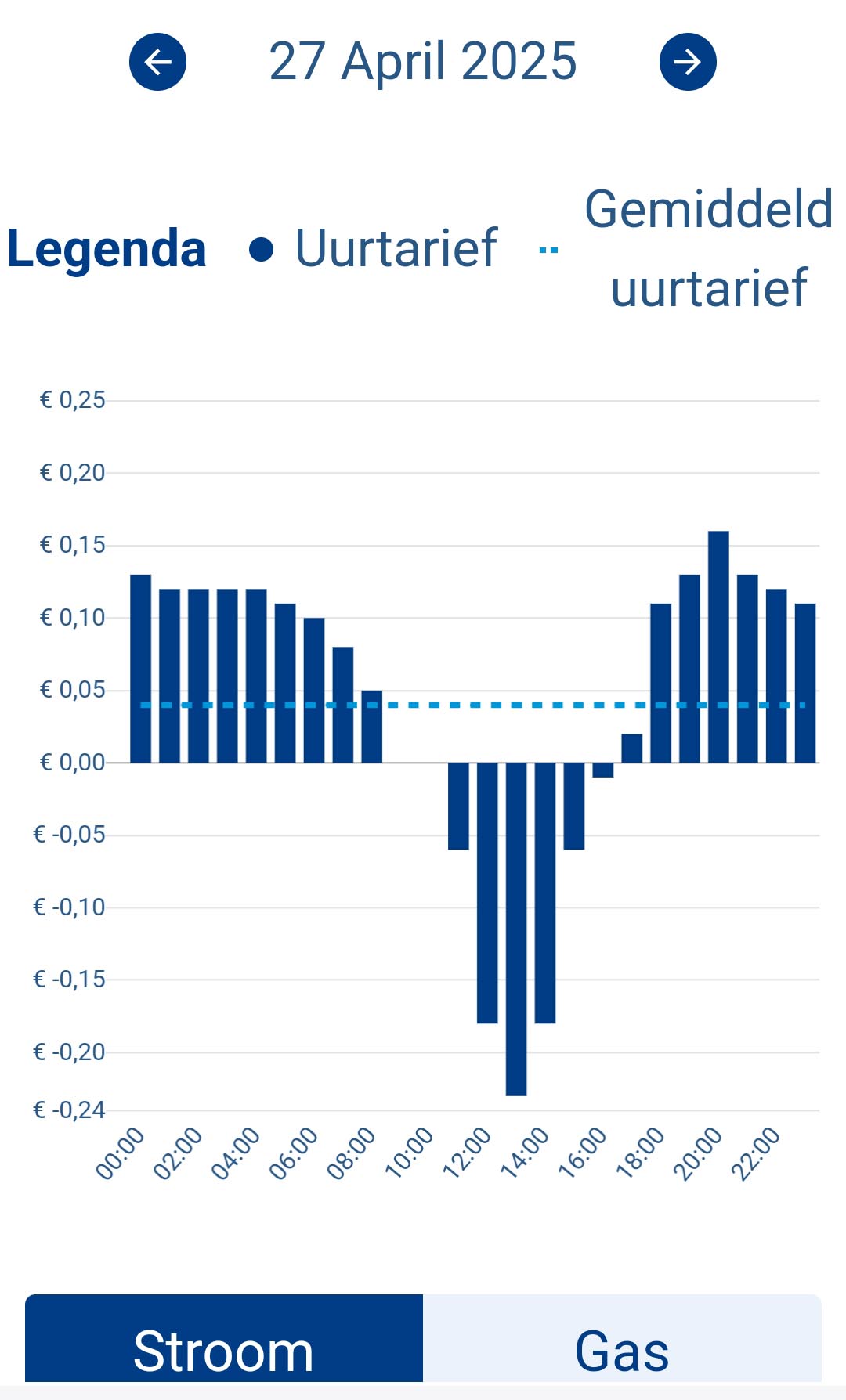
Fig.4 Bron: ANWB Energie
Op 27 april 2025 (1 dag vóór de stroomuitval in Spanje en Portugal) leverde de in ons land opgewekte stroom van 10u tot 18u niets meer op. Er werd zelfs bijbetaald als je stroom afnam, tot zelfs € 0,23 per kWh. In werkelijkheid is de overproductie van stroom door zon en wind nog groter, omdat in dergelijke situaties een deel van de windmolens stilgezet worden. Aan de buurlanden (waaraan ons net gekoppeld is) kunnen we op dergelijke momenten onze overcapaciteit ook niet kwijt, omdat die met dezelfde problemen te maken hebben.
De overheid en netbeheerders proberen ongelukken te voorkomen door de burgers te vragen om minder stroom te gebruiken tussen 16u en 21u. Ook stopt vanaf 1 januari 2027 de salderingsregeling, waardoor je de terug geleverde stroom niet meer automatisch kunt verrekenen met je verbruik. Dat zijn allemaal tekenen dat de grenzen van wat het stroomnet aan kan bereikt zijn.
We zagen al dat het zwakke punt bij stroomopwekking door wind en zon frequentieregeling en inertie zijn. Daar komt voor Nederland nog een derde probleem bij: het stroomnet zit vol.
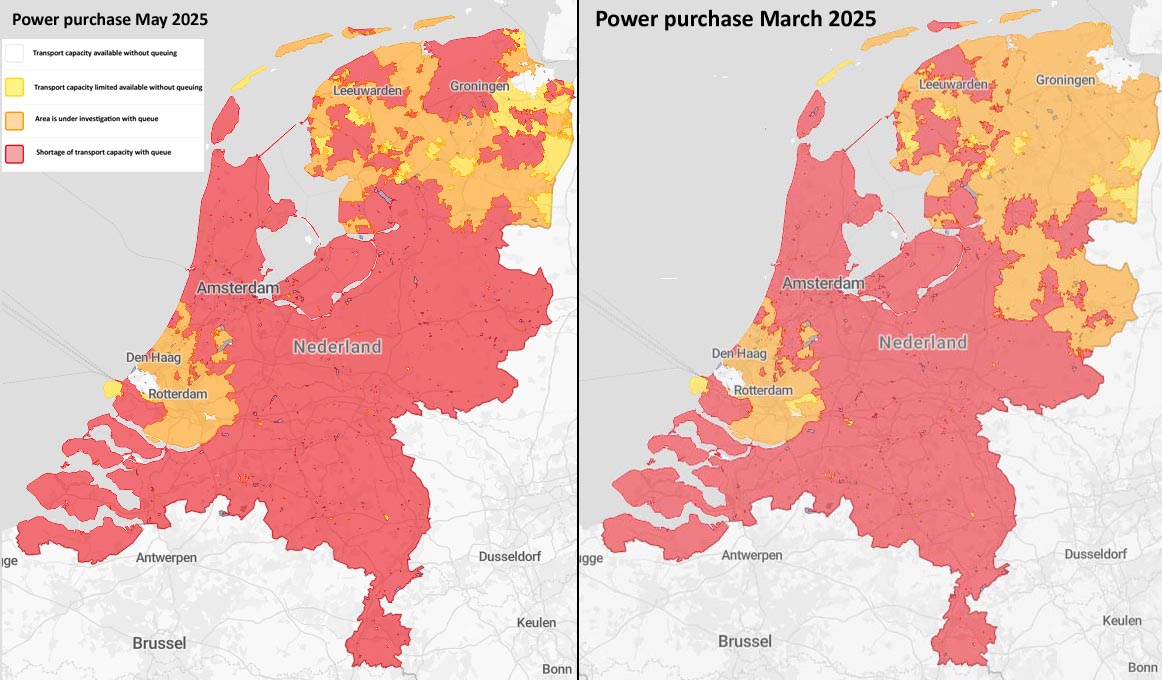
Fig.5 Bron: https://data.partnersinenergie.nl/
Figuur 5 links toont de capaciteitskaart van het elektriciteitsnet aan de afnamezijde van stroom in mei 2025. Op een stukje Zuid Holland en delen van de drie noordelijke provincies zit het net vol. Rood is tekort aan transportcapaciteit met wachtrij, oranje is gebied in onderzoek met wachtrij. Dat is dus nagenoeg geheel Nederland. Om te laten zien hoe snel dat dichtslibben aan de afnamekant gaat toont figuur 5 rechts de situatie in maart 2025, dus 2 maanden eerder. Vooral in Noord Nederland slibt het net razendsnel dicht.
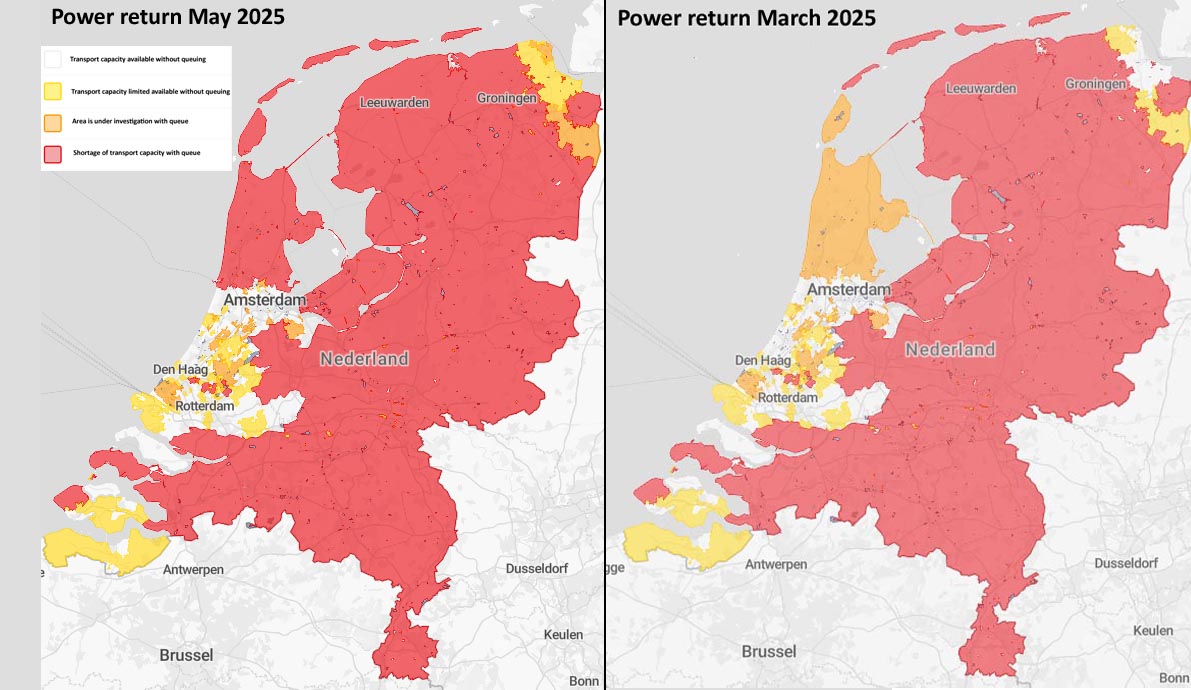
Fig.6 Bron: https://data.partnersinenergie.nl/
Figuur 6 links toont de huidige situatie aan de terugleverzijde van het net. Op een deel van de Randstad en zuidelijk Zeeland na kan er vrijwel nergens meer in Nederland stroom aan het net geleverd worden. Het net zit ook aan deze zijde bomvol. Let eens op het verschil met de situatie in maart 2025 (figuur 6 rechts): heel Noord-Holland heeft de kleur rood gekregen, zoals bijna heel Nederland die al heeft.
Op korte termijn is aan die situatie niets te doen, op langere termijn (enkele decennia) wel door het netwerk te versterken. Maar dat kost geld, zeer veel geld. Beraamd zijn die kosten op 195 miljard euro, zoals altijd op te brengen door brave belastingbetalers. En u weet wat er met de hoogte van geraamde kosten meestal gebeurt, ze gaan zelden omlaag.
Conclusie: we zijn met de energietransitie in ons land het randje van de afgrond genaderd. De stroomuitval in Spanje en Portugal laat zien wat er gebeurt als het echt mis gaat. Binnen enkele seconden kan de stroomleverantie uitvallen. Inzet van zon en wind kent dus zijn grenzen, en die lijken bereikt. Nu stoppen met nóg meer zonnepanelen en windmolens lijkt me beslist noodzakelijk. Maar dat is in de politiek helaas geen populair standpunt. Dat wordt het pas als het mis gaat en het stemmen gaat kosten.
